题目内容
已知函数f(x)=
.
(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若a>0,函数h(x)=xf(x)-x-ax2在(0,2)上有极值,求实数a的取值范围.
| lnx |
| x |
(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若a>0,函数h(x)=xf(x)-x-ax2在(0,2)上有极值,求实数a的取值范围.
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求导,根据导数判断函数的单调性即可.
(2)求导数,由函数h(x)=x•f(x)-x-ax2在(0,2)上有极值,可得2ax2+x-1=0在(0,2)有单根(不能为重根,即a≠-
),即可求实数a的取值范围.
(2)求导数,由函数h(x)=x•f(x)-x-ax2在(0,2)上有极值,可得2ax2+x-1=0在(0,2)有单根(不能为重根,即a≠-
| 1 |
| 8 |
解答:
解:(1)∵f(x)=
,
∴f′(x)=
,
令f′(x)=0,解得x=e,
当f′(x)>0时,即0<x<e,时,函数f(x)单调递增,
当f′(x)<0时,即x>e,时,函数f(x)单调递减,
故函数f(x)在(0,e)上递增,再(e,+∞)上递减.
(2)∵h(x)=lnx-x-ax2
∴h′(x)=
-1-2ax=
=-
∵函数h(x)=x•f(x)-x-ax2在(0,2)上有极值,
∴2ax2+x-1=0在(0,2)有单根(不能为重根,即a≠-
),
由a=
=
(
-
)2-
,
∵
>
>0,∴有a>-
,
∴a的取值范围是a>0.
| lnx |
| x |
∴f′(x)=
| 1-lnx |
| x2 |
令f′(x)=0,解得x=e,
当f′(x)>0时,即0<x<e,时,函数f(x)单调递增,
当f′(x)<0时,即x>e,时,函数f(x)单调递减,
故函数f(x)在(0,e)上递增,再(e,+∞)上递减.
(2)∵h(x)=lnx-x-ax2
∴h′(x)=
| 1 |
| x |
| 1-x-2ax2 |
| x |
| 2ax2+x-1 |
| x |
∵函数h(x)=x•f(x)-x-ax2在(0,2)上有极值,
∴2ax2+x-1=0在(0,2)有单根(不能为重根,即a≠-
| 1 |
| 8 |
由a=
| 1-x |
| 2x2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 8 |
∵
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 8 |
∴a的取值范围是a>0.
点评:本题考查利用导数研究函数的极值,考查学生分析解决问题的能力,属于中档题

练习册系列答案
相关题目
为了弘扬孝道感恩的美德,某学校准备组织一批学生观看亲情励志电影《孝女彩金》.现有10张《孝女彩金》的电影票分给6个班的学生去观看,每个班至少分一张电影票,则不同的分法有( )种.
| A、60 | B、64 |
| C、126 | D、253 |
下列说法正确的有几个( )
①两组对边分别相等的四边形确定一个平面
②和同一条直线异面的两直线一定共面
③与两异面直线分别相交的两直线一定不平行
④一条直线和两平行线中的一条相交,也必定和另一条相交
⑤空间不同三点确定一个平面.
①两组对边分别相等的四边形确定一个平面
②和同一条直线异面的两直线一定共面
③与两异面直线分别相交的两直线一定不平行
④一条直线和两平行线中的一条相交,也必定和另一条相交
⑤空间不同三点确定一个平面.
| A、1 | B、2 | C、3 | D、4 |
 一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )
一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )A、
| ||||||||
B、3
| ||||||||
C、3
| ||||||||
D、
|
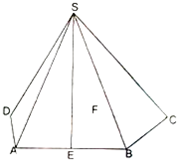 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.