题目内容
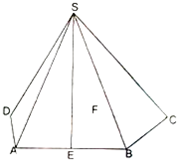 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.(1)求证:平面SEF⊥平面ABCD;
(2)若平面SAB∩平面SCD=l,试问l与平面ABCD是否平行,并说明理由.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)欲证平面SEF⊥平面ABCD,根据面面垂直的判定定理可知在平面ABCD内一直线与平面SEF垂直,而根据线面垂直的性质定理可知AB⊥平面SEF;
(2)根据线面平行的判定定理可知AB∥平面SCD,而平面SAB∩平面SCD=l,再根据直线与平面平行的性质定理得AB∥l,即可证明l∥平面ABCD.
(2)根据线面平行的判定定理可知AB∥平面SCD,而平面SAB∩平面SCD=l,再根据直线与平面平行的性质定理得AB∥l,即可证明l∥平面ABCD.
解答:
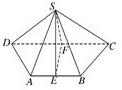 (1)证明:由SA=SB,E为AB中点得SE⊥AB.由SC=SD,F为CD中点得SF⊥DC.又AB∥DC,∴AB⊥SF.
(1)证明:由SA=SB,E为AB中点得SE⊥AB.由SC=SD,F为CD中点得SF⊥DC.又AB∥DC,∴AB⊥SF.
又SF∩SE=S,∴AB⊥平面SEF.
又∵AB?平面ABCD,
∴平面SEF⊥平面ABCD.
(2)解:∵AB∥CD,CD?面SCD,
∴AB∥平面SCD.
又∵平面SAB∩平面SCD=l,
根据直线与平面平行的性质定理得AB∥l.
∵l?平面ABCD,AB?平面ABCD,
∴l∥平面ABCD.
 (1)证明:由SA=SB,E为AB中点得SE⊥AB.由SC=SD,F为CD中点得SF⊥DC.又AB∥DC,∴AB⊥SF.
(1)证明:由SA=SB,E为AB中点得SE⊥AB.由SC=SD,F为CD中点得SF⊥DC.又AB∥DC,∴AB⊥SF.又SF∩SE=S,∴AB⊥平面SEF.
又∵AB?平面ABCD,
∴平面SEF⊥平面ABCD.
(2)解:∵AB∥CD,CD?面SCD,
∴AB∥平面SCD.
又∵平面SAB∩平面SCD=l,
根据直线与平面平行的性质定理得AB∥l.
∵l?平面ABCD,AB?平面ABCD,
∴l∥平面ABCD.
点评:本小题主要考查平面与平面垂直的判定,以及线面平行的判定定理和性质定理等有关知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
| A、13 | ||
| B、2 | ||
C、
| ||
D、
|
设集合A={x|
<2x<4},B={x|x2≤1},则A∪B=( )
| 1 |
| 2 |
| A、{x|x<2} | ||
B、{x|-
| ||
| C、{x|-1≤x<2} | ||
| D、{x|1≤x<2} |