题目内容
下列说法正确的有几个（ ）
①两组对边分别相等的四边形确定一个平面
②和同一条直线异面的两直线一定共面
③与两异面直线分别相交的两直线一定不平行
④一条直线和两平行线中的一条相交，也必定和另一条相交
⑤空间不同三点确定一个平面．
①两组对边分别相等的四边形确定一个平面
②和同一条直线异面的两直线一定共面
③与两异面直线分别相交的两直线一定不平行
④一条直线和两平行线中的一条相交，也必定和另一条相交
⑤空间不同三点确定一个平面．
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用
专题：空间位置关系与距离
分析：分别对每个命题进行判断，正确的需要证明，如③，错误的举反例即可，如①②④⑤．
解答：
解：如下图
对于①，在正四面体A-BCD中，空间四边形ABCD的对边AB=CD
但ABCD四点不共面．故①是错误的命题．
对于②，在正方体A-C1中，直线AA1与BC都是直线AB的异面直线，同样，AA1与BC也是异面直线，故②是错误的命题．
对于③是正确的，设直线AB与CD是异面直线，则直线AC与BD一定不平行．否则AC∥BD，则AC与BD确定一个平面α，则AC?α，BD?α，∴A∈α，B∈α，C∈α，D∈α，∴AB?α，CD?α，这与假设矛盾，故原命题正确．
对于④，在正方体A-C1中，AB∥CD，而直线AA1与直线AB相交，但与直线CD不相交．故④是错误的
对于⑤，共线的三点就不能确定一个平面，经过三点的平面有无穷之多．个⑤是错误的．
综上，只有命题③是正确的．
故答案为：A
解：如下图对于①，在正四面体A-BCD中，空间四边形ABCD的对边AB=CD
但ABCD四点不共面．故①是错误的命题．
对于②，在正方体A-C1中，直线AA1与BC都是直线AB的异面直线，同样，AA1与BC也是异面直线，故②是错误的命题．
对于③是正确的，设直线AB与CD是异面直线，则直线AC与BD一定不平行．否则AC∥BD，则AC与BD确定一个平面α，则AC?α，BD?α，∴A∈α，B∈α，C∈α，D∈α，∴AB?α，CD?α，这与假设矛盾，故原命题正确．
对于④，在正方体A-C1中，AB∥CD，而直线AA1与直线AB相交，但与直线CD不相交．故④是错误的
对于⑤，共线的三点就不能确定一个平面，经过三点的平面有无穷之多．个⑤是错误的．
综上，只有命题③是正确的．
故答案为：A
点评：本题以命题的形式考查了空间直线的位置关系，属于基础题．
练习册系列答案
相关题目
设集合A={x|
＜2x＜4}，B={x|x2≤1}，则A∪B=（ ）
| 1 |
| 2 |
| A、{x|x＜2} | ||
B、{x|-
| ||
| C、{x|-1≤x＜2} | ||
| D、{x|1≤x＜2} |
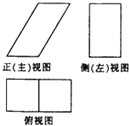一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
某多面体的三视图如图所示，则此多面体的体积为（ ）| A、6 | B、9 | C、12 | D、18 |
已知回归直线方程
=
+
x，如果x=3时，y的估计值是17，x=8时，y的估计值是22，那么回归直线方程是（ ）
 |
| y |
|
| a |
|
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|