题目内容
已知sin(α+
)=
,则cos(
-α)的值为( )
| π |
| 3 |
| 3 |
| 5 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:原式中的角度变形后,利用诱导公式化简,将已知等式代入计算即可求出值.
解答:
解:∵sin(α+
)=
,
∴cos(
-α)=cos[
-(α+
)]=sin(α+
)=
.
故选:C.
| π |
| 3 |
| 3 |
| 5 |
∴cos(
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 5 |
故选:C.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
| 1 |
| 3 |
| ∫ |
-
|
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
如图,在菱形ABCD中,∠DAB=120°,则以下说法错误的是( )
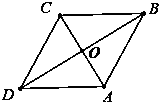

A、与
| ||||||
B、与
| ||||||
C、
| ||||||
D、
|
直线y=x是曲线y=a+lnx的一条切线,则实数a的值为( )
| A、-1 | B、e | C、ln2 | D、1 |
已知△ABC的顶点A(0,0),B(4,0),且AC边上的中线BD的长为3,则顶点C的轨迹方程是( )
| A、(x-8)2+y2=36(y≠0) |
| B、(x-4)2+y2=9(y≠0) |
| C、x2+y2=9(y≠0) |
| D、3x+4y-12=0(y≠0) |
函数y=sin2x-3sinx+2的最小值是( )
| A、2 | ||
| B、0 | ||
C、-
| ||
| D、6 |
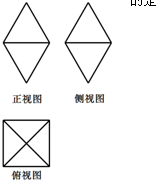 如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为
如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为