题目内容
已知△ABC的顶点A(0,0),B(4,0),且AC边上的中线BD的长为3,则顶点C的轨迹方程是( )
| A、(x-8)2+y2=36(y≠0) |
| B、(x-4)2+y2=9(y≠0) |
| C、x2+y2=9(y≠0) |
| D、3x+4y-12=0(y≠0) |
考点:轨迹方程
专题:计算题,直线与圆
分析:确定C,D坐标之间的关系,利用AC边上的中线BD的长为3,即可求出顶点C的轨迹方程.
解答:
解:设C(x,y)(y≠0),则D(
,
),
∵B(4,0),且AC边上的中线BD的长为3,
∴(
-4)2+(
)2=9,
即(x-8)2+y2=36(y≠0).
故选:A.
| x |
| 2 |
| y |
| 2 |
∵B(4,0),且AC边上的中线BD的长为3,
∴(
| x |
| 2 |
| y |
| 2 |
即(x-8)2+y2=36(y≠0).
故选:A.
点评:本题主要考查了轨迹方程的问题.本题解题的关键是正确运用代入法.

练习册系列答案
相关题目
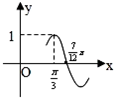 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先向右平移
| ||||
D、先向右平移
|
已知sin(α+
)=
,则cos(
-α)的值为( )
| π |
| 3 |
| 3 |
| 5 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
函数y=4sin(2x-
)的图象的一个对称中心是( )
| π |
| 6 |
A、(
| ||
B、(
| ||
C、(-
| ||
D、(
|
在等差数列{an}中,已知a6+a7=3,则S12=( )
| A、18 | B、21 | C、36 | D、39 |
下列四个函数中,既是(0,
)上的增函数,又是以π为周期的偶函数的是( )
| π |
| 2 |
| A、y=tanx |
| B、y=|sinx| |
| C、y=cosx |
| D、y=|cosx| |
在△ABC中,有a2+b2-c2=ab,则角C为( )
| A、60° | B、120° |
| C、30° | D、45°或135° |