题目内容
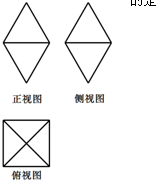 如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为
如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为
| ||
| 2 |
A、
| ||
B、2
| ||
C、4
| ||
| D、4 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体是两个底面相对的正四棱锥的组合体,根据正视图、侧视图都是面积及形状可得底面正方形的边长及侧面上的斜高,代入八面体的表面积公式计算.
解答:
解:由三视图知:几何体是两个底面相对的正四棱锥的组合体,设四棱锥底面正方形的边长为a,
由正视图、侧视图都是面积为
且一个内角为60°的菱形得,2×
×a×a×
=
⇒a=1,
∴四棱锥侧面上的斜高为1,
∴几何体的表面积S=8×
×1×1=4.
故选:D.
由正视图、侧视图都是面积为
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴四棱锥侧面上的斜高为1,
∴几何体的表面积S=8×
| 1 |
| 2 |
故选:D.
点评:本题考查了由三视图求几何体的表面积,根据三视图求相关几何量的数据是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数m(3+i)-(2+i)(m∈R,i为虚数单位)在复平面内对应的点不可能位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f(x+1)=x2-x+3,那么f(x-1)的表达式是( )
| A、x2-5x+9 |
| B、x2-x-3 |
| C、x2+5x-9 |
| D、x2-x+1 |
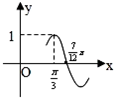 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先向右平移
| ||||
D、先向右平移
|
已知sin(α+
)=
,则cos(
-α)的值为( )
| π |
| 3 |
| 3 |
| 5 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
在△ABC中,有a2+b2-c2=ab,则角C为( )
| A、60° | B、120° |
| C、30° | D、45°或135° |