题目内容

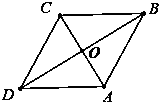
如图，在菱形ABCD中，∠DAB=120°，则以下说法错误的是（　　）
A、与
AB
相等的向量只有一个（不含
AB
）
B、与
AB
的模相等的向量有9个（不含
AB
）
C、
BD
的模恰为
DA
模的
3
倍
D、
CB
与
DA
不共线
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：A．与
AB
相等的向量只有一个（不含
AB
）是
DC
；
B．在菱形ABCD中，∠DAB=120°，可得∠ADC=60°，△ADC和△ABC都是等边三角形．
可得：与
AB
的模相等的向量有9个（不含
AB
）：
BA
，
CD
，
DC
，
AC
，
CA
，
AD
，
DA
，
BC
，
CB
．
C．由等边三角形的性质可得：|
OD
|=
3
2
|
DA
|，即可得出|
BD
|=2|
OD
|=
3
|
DA
|．
D．由于
CB
=
DA
，可得
CB
与
DA
共线．
解答： 解：A．与
AB
相等的向量只有一个（不含
AB
）是
DC
，正确；
B．在菱形ABCD中，∠DAB=120°，∴∠ADC=60°，因此△ADC和△ABC都是等边三角形．
∴与
AB
的模相等的向量有9个（不含
AB
）：
BA
，
CD
，
DC
，
AC
，
CA
，
AD
，
DA
，
BC
，
CB
．因此正确．
C．由等边三角形的性质可得：|
OD
|=
3
2
|
DA
|，∴|
BD
|=2|
OD
|=
3
|
DA
|．
因此
BD
的模恰为
DA
模的
3
倍，故正确．
D．∵
CB
=
DA
，∴
CB
与
DA
共线，故D不正确．
综上可知：只有D不正确．
故选：D．
点评：本题考查了向量相等、共线、模相等等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
如图，已知函数y=Asin（ωx+φ）（ω＞0）的图象（的部分），则函数的表达式为
 
复数m（3+i）-（2+i）（m∈R，i为虚数单位）在复平面内对应的点不可能位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
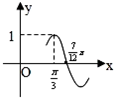已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则y=f（x）的图象可由函数g（x）=sinx的图象（纵坐标不变）（　　）
A、先把各点的横坐标缩短到原来的
1
2
倍，再向右平移
π
6
个单位
B、先把各点的横坐标伸长到原来的2倍，再向右平移
π
12
个单位
C、先向右平移
π
12
个单位，再把各点的横坐标伸长到原来的2倍
D、先向右平移
π
6
个单位，再把各点的横坐标缩短到原来的
1
2
倍
给定命题p：存在x∈R，使
a
=x
b
，则
a
∥
b
；q：?锐角△ABC，sinA＜cosB．下面复合命题中正确的是（　　）
A、p∧qB、p∨q
C、￢p∧qD、￢p∨q
已知sin（α+
π
3
）=
3
5
，则cos（
π
6
-α）的值为（　　）
A、
1
6
B、
3
4
C、
3
5
D、-
3
5
函数y=4sin（2x-
π
6
）的图象的一个对称中心是（　　）
A、（
π
12
，0）
B、（
π
3
，0）
C、（-
π
6
，0）
D、（
π
6
，0）
下列四个函数中，既是（0，
π
2
）上的增函数，又是以π为周期的偶函数的是（　　）
A、y=tanx
B、y=|sinx|
C、y=cosx
D、y=|cosx|
已知函数f（x）=2x-log
1
2
x实数a，b，c满足a＜b＜c，且满足f（a）•f（b）•f（c）＜0，若实数x0是函数y=f（x）的一个零点，则下列结论一定成立的是（　　）
A、x0＞c
B、x0＜c
C、x0＞a
D、x0＜a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网