题目内容
| 1 |
| 3 |
| ∫ |
-
|
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:定积分
专题:计算题,导数的综合应用
分析:由于cos2x的一个原函数为
sin2x故根据牛顿-莱布尼茨公式即可求解.
| 1 |
| 2 |
解答:
解:
cos2xdx=
×
sin2x
=
(sin
-sin(-
))=
.
故选A
| 1 |
| 3 |
| ∫ |
-
|
| 1 |
| 3 |
| 1 |
| 2 |
| | |
-
|
| 1 |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
故选A
点评:本题主要考查了定积分的计算.解题的关键是要能求出被积函数的一个原函数然后再根据牛顿-莱布尼茨公式求解.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数f(x+1)=x2-x+3,那么f(x-1)的表达式是( )
| A、x2-5x+9 |
| B、x2-x-3 |
| C、x2+5x-9 |
| D、x2-x+1 |
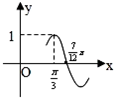 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先向右平移
| ||||
D、先向右平移
|
下列积分值为2的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知sin(α+
)=
,则cos(
-α)的值为( )
| π |
| 3 |
| 3 |
| 5 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
在等差数列{an}中,已知a6+a7=3,则S12=( )
| A、18 | B、21 | C、36 | D、39 |
已知在数列{an}中,a1=1,an+1-an=2(n∈N*),则an为( )
| A、n2-1 |
| B、n2 |
| C、2n |
| D、2n-1 |