题目内容
已知函数f(x)=lnx-ax(a∈R).
(I)若曲线y=f(x)在点(1,f(1))处的切线与直线x-y+1=0垂直,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若a=1,函数b≠0,函数g(x)=
bx3-bx,如果对任意的x1∈(1,2),总存在x2∈(1,2),使得f(x1)=g(x2),求实数b的取值范围.
(I)若曲线y=f(x)在点(1,f(1))处的切线与直线x-y+1=0垂直,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若a=1,函数b≠0,函数g(x)=
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,导数的概念及应用,导数的综合应用
分析:(Ⅰ)求出函数的导数,求得切线的斜率,由两直线垂直的条件,即可得到a;
(Ⅱ)求出导数,对a讨论,a≤0,a>0分别令导数大于0,得增区间,令导数小于0,得减区间,注意定义域即可得到单调区间;
(Ⅲ)求出f(x)在(1,2)内的值域,讨论b>0,b<0,求出g(x)的值域,由已知得到f(x)的值域包含在g(x)的值域,即可得到b的范围.
(Ⅱ)求出导数,对a讨论,a≤0,a>0分别令导数大于0,得增区间,令导数小于0,得减区间,注意定义域即可得到单调区间;
(Ⅲ)求出f(x)在(1,2)内的值域,讨论b>0,b<0,求出g(x)的值域,由已知得到f(x)的值域包含在g(x)的值域,即可得到b的范围.
解答:
解:(Ⅰ)函数f(x)=lnx-ax的导数为f′(x)=
-a,
则在点(1,f(1))处的切线斜率为1-a,
由于切线与直线x-y+1=0垂直,则1-a=-1,
则a=2;
(Ⅱ)f′(x)=
-a=
(x>0),
当a≤0时,f′(x)>0,f(x)在(0,+∞)上递增,
当a>0时,f′(x)>0时,0<x<
,f′(x)<0时,x>
.
综上,a≤0时,f(x)只有增区间:(0,+∞),
a>0时,f(x)的增区间是(0,
),减区间为(
,+∞);
(Ⅲ)a=1时,f(x)=lnx-x,由(Ⅱ)知f(x)在(1,2)上递减,则f(x)的值域为(ln2-2,-1),
由于g(x)=
bx3-bx的导数为g′(x)=b(x2-1),
则当b>0时,g′(x)>0,g(x)在(1,2)上递增,g(x)的值域为(-
b,
b);
当b<0时,g′(x)<0,g(x)在(1,2)上递减,g(x)的值域为(
b,-
b);
由于对任意的x1∈(1,2),总存在x2∈(1,2),使得f(x1)=g(x2),
则b>0时,(ln2-2,-1)⊆(-
b,
b),则有-
b≤ln2-2,即有b≥3-
ln2;
b<0时,(ln2-2,-1)⊆(
b,-
b),则有
b≤ln2-2,即有b≥
ln2-3.
综上,可得实数b的取值范围是(-∞≥
ln2-3]∪[3-
ln2,+∞).
| 1 |
| x |
则在点(1,f(1))处的切线斜率为1-a,
由于切线与直线x-y+1=0垂直,则1-a=-1,
则a=2;
(Ⅱ)f′(x)=
| 1 |
| x |
| 1-ax |
| x |
当a≤0时,f′(x)>0,f(x)在(0,+∞)上递增,
当a>0时,f′(x)>0时,0<x<
| 1 |
| a |
| 1 |
| a |
综上,a≤0时,f(x)只有增区间:(0,+∞),
a>0时,f(x)的增区间是(0,
| 1 |
| a |
| 1 |
| a |
(Ⅲ)a=1时,f(x)=lnx-x,由(Ⅱ)知f(x)在(1,2)上递减,则f(x)的值域为(ln2-2,-1),
由于g(x)=
| 1 |
| 3 |
则当b>0时,g′(x)>0,g(x)在(1,2)上递增,g(x)的值域为(-
| 2 |
| 3 |
| 2 |
| 3 |
当b<0时,g′(x)<0,g(x)在(1,2)上递减,g(x)的值域为(
| 2 |
| 3 |
| 2 |
| 3 |
由于对任意的x1∈(1,2),总存在x2∈(1,2),使得f(x1)=g(x2),
则b>0时,(ln2-2,-1)⊆(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
b<0时,(ln2-2,-1)⊆(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
综上,可得实数b的取值范围是(-∞≥
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查导数的运用:求切线方程和单调区间,考查函数的单调性和运用:求最值和值域,考查任意和存在问题转化为值域的包含关系,属于中档题和易错题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列函数为偶函数且在(0,+∞)为增函数的是( )
| A、y=-|x| | ||
| B、y=x3 | ||
| C、y=ex | ||
D、y=ln
|
已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(2015)=( )
| A、2 | B、-2 | C、8 | D、-8 |
设f(x)是[-1,1]上的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-
)=( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
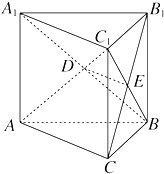 如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.
如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.