题目内容
数列{an}的通项公式为an=n2+λn,对于任意自然数n(n≥1)都是递增数列,则实数λ的取值范围为 .
考点:数列的函数特性
专题:函数的性质及应用
分析:数列{an}的通项公式为an=n2+λn,对于任意自然数n(n≥1)都是递增数列,根据函数对称性,单调性,可知:-
<
,可得范围.
| λ |
| 2 |
| 3 |
| 2 |
解答:
解:∵数列{an}的通项公式为an=n2+λn,对于任意自然数n(n≥1)都是递增数列,
∴根据二次函数的性质可得:
-
<
,即λ>-3,
故答案为:λ>-3
∴根据二次函数的性质可得:
-
| λ |
| 2 |
| 3 |
| 2 |
故答案为:λ>-3
点评:本题考查了数列的函数的性质,根据二次函数的单调性,对称性求解.

练习册系列答案
相关题目
 如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )
如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
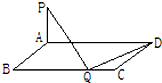 已知在矩形ABCD中,AB=2
已知在矩形ABCD中,AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|