题目内容
已知数列{an}满足a1=a>0,前n项和为Sn,Sn=
(1+an).
(1)求证:{an}是等比数列;
(2)记bn=an1n|an|(n∈N*),当a=
时是否存在正整数n,都有bn≤bm?如果存在,求出m的值;如果不存在,请说明理由.
| a |
| 1+a |
(1)求证:{an}是等比数列;
(2)记bn=an1n|an|(n∈N*),当a=
| ||
| 5 |
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由已知推导出an•
=an-an-1,an=-a•an-1(n≥2),由此能证明{an}是等比数列.
(2)由an=(-1)n-1an,bn=(-1)n-1nanlna,得若存在满足条件的正整数m,则m为偶数,b2k+2-b2k=-(2k+2)(a2-
)a2klna.(k∈N*),由此能求出存在m=4,满足题意.
| 1+a |
| a |
(2)由an=(-1)n-1an,bn=(-1)n-1nanlna,得若存在满足条件的正整数m,则m为偶数,b2k+2-b2k=-(2k+2)(a2-
| 2k |
| 2k+2 |
解答:
(1)证明:∵Sn=
(1+an),
∴Sn-1=
(1+an-1).
两式相减得an•
=an-an-1,an=-a•an-1(n≥2),
故{an}是等比数列.
(2)解:an=(-1)n-1an,bn=(-1)n-1nanlna,
∵lna<0,∴b2k>0,b2k+1<0(k∈N*),
若存在满足条件的正整数m,则m为偶数,
b2k+2-b2k=-(2k+2)(a2-
)a2klna.(k∈N*),
当
>
,即k>
时,b2k+2<b2k,
又b4>b2,k≥2时b4>b6>b8>…
∴存在m=4,满足题意.
| a |
| 1+a |
∴Sn-1=
| a |
| 1+a |
两式相减得an•
| 1+a |
| a |
故{an}是等比数列.
(2)解:an=(-1)n-1an,bn=(-1)n-1nanlna,
∵lna<0,∴b2k>0,b2k+1<0(k∈N*),
若存在满足条件的正整数m,则m为偶数,
b2k+2-b2k=-(2k+2)(a2-
| 2k |
| 2k+2 |
当
| 2k |
| 2k+2 |
| 3 |
| 5 |
| 3 |
| 2 |
又b4>b2,k≥2时b4>b6>b8>…
∴存在m=4,满足题意.
点评:本题考查等比数列的证明,考查满足条件的实数值的求法,解题时要认真审题,注意迭代法的合理运用,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
在数列{an}中,a1=3,an+1=an+lg(1+
)(n∈N*),则an=( )
| 1 |
| n |
| A、lgn | ||||||
B、3+lg(
| ||||||
| C、3+lgn | ||||||
| D、3+3lng |
若函数f(x)=2x3-9x2+12x-a恰好有两上不同零点,则a的值为( )
| A、4 | B、5或6 |
| C、4或5 | D、4或6 |
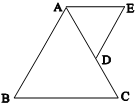 如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,| BD |
| CE |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
等差数列{an}中,a1=3,a3=9,若ak=243,则k等于( )
| A、79 | B、80 | C、81 | D、82 |
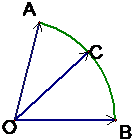 给定两个长度为1的平面向量
给定两个长度为1的平面向量
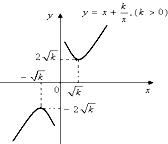 函数f(x)=x+
函数f(x)=x+