题目内容
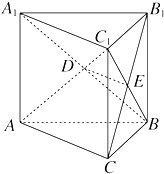 如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.
如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.考点:棱柱、棱锥、棱台的体积
专题:
分析:由VA-BB1C=VB1-ABC,得S△B1EB=
S△BB1C,且A到面BB1C的距离h为D到面B1EB的2倍,由此能求出四面体B-B1DE的体积.
| 1 |
| 2 |
解答:
解:VA-BB1C=VB1-ABC=
S△ABC•B1B=
•
a2•a=
a3.
由条件知,D、E分别为AB1和CB1的中点,
∴S△B1EB=
S△BB1C,且A到面BB1C的距离h为D到面B1EB的2倍,即D到B1EB的距离为
h.
∵VD-B1EB=
S△B1EB•
h
=
•(S△BB1E•
)•
h
=
•
S△BB1C•h
=
VA-BB1C
=
•
a3
=
a3.
∴VD-B1EB=
a3.
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |

由条件知,D、E分别为AB1和CB1的中点,
∴S△B1EB=
| 1 |
| 2 |
| 1 |
| 2 |
∵VD-B1EB=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 3 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
| ||
| 12 |
=
| ||
| 48 |
∴VD-B1EB=
| ||
| 48 |
点评:本题考查四面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
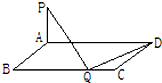 已知在矩形ABCD中,AB=2
已知在矩形ABCD中,AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|
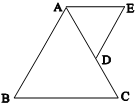 如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,| BD |
| CE |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|