题目内容
1.已知A(2,0),直线4x+3y+1=0被圆C:(x+3)2+(y-m)2=13(m<3)所截得的弦长为4$\sqrt{3}$,且P为圆C上任意一点.(1)求|PA|的最大值与最小值;
(2)圆C与坐标轴相交于三点,求以这三个点为顶点的三角形的内切圆的半径.
分析 (1)利用直线4x+3y+1=0被圆C:(x+3)2+(y-m)2=13(m<3)所截得的弦长为4$\sqrt{3}$,求出m,即可求|PA|的最大值与最小值;
(2)求出圆C与坐标轴相交于三点的坐标,再求以这三个点为顶点的三角形的内切圆的半径.
解答 解:(1)∵直线4x+3y+1=0被圆C:(x+3)2+(y-m)2=13(m<3)所截得的弦长为4$\sqrt{3}$,
∴圆心到直线的距离d=$\frac{|-12+3m+1|}{5}$=1,
∵m<3,∴m=2,
∴AC=$\sqrt{29}$,
∴|PA|的最大值与最小值分别为$\sqrt{29}$+$\sqrt{13}$,$\sqrt{29}$-$\sqrt{13}$;
(2)由(1)可得圆的方程:(x+3)2+(y-2)2=13,
令x=0,则y=0或4,令y=0,则x=0或-6,
∴圆C与坐标轴相交于三点M(0,4),O(0,0),B(-6,0),
∴△MON为直角三角形,斜边|MN|=2$\sqrt{13}$,内切圆的半径为$\frac{4+6-2\sqrt{13}}{2}$=5-$\sqrt{13}$.
点评 本题考查直线与圆位置关系的运用,考查内切圆半径的求解,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
12.某工厂生产某种产品,用传送带将产品送至下一工序,质量员每隔10分钟在传送带某一位置取一件产品进行检验,这种抽样的方法为( )
| A. | 分层抽样 | B. | 简单随机抽样 | C. | 系统抽样 | D. | 其它抽样方式 |
9.曲线y=4x+x2在点(-1,-3)处的切线方程是( )
| A. | y=7x+4 | B. | y=7x+2 | C. | y=x-4 | D. | y=2x-1 |
16.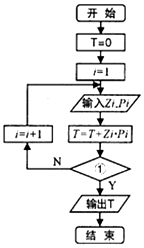 某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
 某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率| 组别(i) | 睡眠时间 | 组中值(Zi) | 频数 | 频率(Pi) |
| 1 | [4.5,5.5) | 5 | 2 | 0.04 |
| 2 | [5.5,6.5) | 6 | 6 | 0.12 |
| 3 | [6.5,7.5) | 7 | 20 | 0.40 |
| 4 | [7.5,8.5) | 8 | 18 | 0.36 |
| 5 | [8.5,9.5) | 9 | 3 | 0.06 |
| 6 | [9.5,10.5) | 10 | 1 | 0.02 |
6.几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题,然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如表:
(1)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
(2)若对年龄在[15,20)的被调查人中随机选取两人进行调查,求恰好这两人都支持发展共享单车的概率.
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如表:
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
参考数据:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{3}x+1,x≤1}\\{lnx,x>1}\end{array}\right.$,若方程f(x)-ax=0恰有两个不同的根,则实数a的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{e}$) | C. | ($\frac{1}{e}$,$\frac{4}{3}$] | D. | (-∞,0]∪[$\frac{4}{3}$,+∞) |
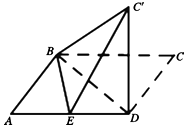 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.