题目内容
10.已知抛物线C:y2=6x的焦点为F,点A(0,m),m>0,射线FA于抛物线C交于点M,与其准线交于点N,若|MN|=2|FM|,则m=3.
分析 求出抛物线C的焦点F的坐标,过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|.Rt△MPN中,根据|PN|=2|PM|,tan∠NMP=-k=2,从而得到AF的斜率k=2.然后求解m的值.
解答 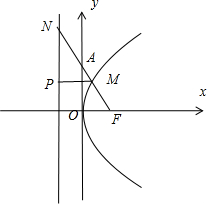 解:∵抛物线C:y2=6x的焦点为F($\frac{3}{2}$,0),点A坐标为(0,m),
解:∵抛物线C:y2=6x的焦点为F($\frac{3}{2}$,0),点A坐标为(0,m),
∴抛物线的准线方程为l:x=-$\frac{3}{2}$,射线FA于抛物线C交于点M,与其准线交于点N,
若|MN|=2|FM|,过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|,
∵Rt△MPN中,tan∠NMP=-k=2,直线AF的斜率为k=-2,
∴直线AF为:y=-2(x-$\frac{3}{2}$),
x=0时,m=3.
故答案为:3.
点评 本题给出抛物线方程和射线FA,利用线段的比值.求解直线的斜率、抛物线的定义、标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
2.l1、l2是空间两条直线,α是平面,以下结论正确的是( )
| A. | 如果l1∥α,l2∥α,则一定有l1∥l2 | B. | 如果l1⊥l2,l2⊥α,则一定有l1⊥α | ||
| C. | 如果l1⊥l2,l2⊥α,则一定有l1∥α | D. | 如果l1⊥α,l2∥α,则一定有l1⊥l2 |
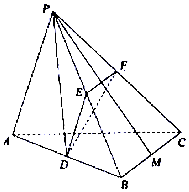 如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.
如图,已知三棱锥P-ABC,BC⊥AC,BC=AC=2,PA=PB,平面PAB⊥平面ABC,D、E、F分别是AB、PB、PC的中点.