题目内容
13. 如图所示,四棱锥P-ABCD,平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点.
如图所示,四棱锥P-ABCD,平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点.(1)求证:PB⊥CB.
(2)记平面ADM与平面PBC的交线是l,试判断直线l与BC的位置关系,并加以证明.
(3)若CD的中点是E,平面PAB上的动点F满足EF∥平面ADM,求在△PAB内满足条件的所有的点F构成的图形.
分析 (1)由平面PAB⊥平面ABCD,CB⊥AB,可得CB⊥平面PAB,即PB⊥CB;
(2)直线l∥BC.根据线面平行的判定与性质可以证明;
(3)取AB中点H,NB中点G,易得EH∥AD,HG∥AN,即可得平面ADM∥平面EHG,可得在△PAB内满足条件的所有的点F构成的图形时线段.
解答 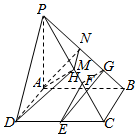 解:(1)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
解:(1)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
CB?平面ABCD,CB⊥AB,∴CB⊥平面PAB,
又PB?平面PAB,∴PB⊥CB,
(2)直线l∥BC.
证明:∵AD∥BC,AD?平面PBC,CB?平面PBC,
∴AD∥平面PBC,
又因为平面ADM∩平面PBC=l,AD?平面ADM,
∴AD∥l∥BC,(如图,∵点M是棱PC的中点,取PB中点N,则MN就是交线l),
(3)取AB中点H,NB中点G,易得EH∥AD,HG∥AN,
即可得平面ADM∥平面EHG,
则点F在线段HG上,∴在△PAB内满足条件的所有的点F构成的图形时线段.
,
点评 本题考查了线线平行的判定、线面平行的判定与性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若实数a、b满足条件a>b,则下列不等式一定成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | ab>b2 | D. | a3>b3 |
2.已知:$x{(x-2)^8}={a_0}+{a_1}(x-1)+{a_2}{(x-1)^2}+…+{a_9}{(x-1)^9}$,则a6=( )
| A. | -28 | B. | -448 | C. | 112 | D. | 448 |
3.已知1<a<b,m=ab-1,n=ba-1,则m,n的大小关系为( )
| A. | m<n | |
| B. | m=n | |
| C. | m>n | |
| D. | m,n的大小关系不确定,与a,b的取值有关 |
 如图,四棱锥中,AB∥CD,BC⊥CD侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
如图,四棱锥中,AB∥CD,BC⊥CD侧面SAB为等边三角形,AB=BC=2,CD=SD=1.