题目内容
3.设函数f(x)=|2x-1|-|x+1|(Ⅰ)解不等式f(x)>2x-1;
(Ⅱ)若存在实数x,使得不等式f(x)≤$\frac{{t}^{2}}{2}$-t-3成立,求t的取值范围.
分析 (Ⅰ)通过讨论x的范围求出不等式的解集即可;(Ⅱ)求出f(x)的最小值,问题转化为关于t的不等式,解出即可.
解答 解:(Ⅰ)f(x)=$\left\{\begin{array}{l}{-x+2,x<-1}\\{-3x,-1≤x≤\frac{1}{2}}\\{x-2,x≥\frac{1}{2}}\end{array}\right.$,
所以f(x)>2x-1?$\left\{\begin{array}{l}{x<-1}\\{-x+2>2x-1}\end{array}\right.$或$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{-3x>2x-1}\end{array}\right.$或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{x-2>2x-1}\end{array}\right.$,
解得x<-1或-1≤x<$\frac{1}{5}$,
所以原不等式解解为{x|x<$\frac{1}{5}$};
(Ⅱ)依题意可知,f(x)min≤$\frac{{t}^{2}}{2}$-t-3,
由(Ⅰ)可知连续函数f(x)在(-∞,-1)和[-1,$\frac{1}{2}$]上是减函数,在($\frac{1}{2}$,+∞)上是增函数,
所以f(x)min=f($\frac{1}{2}$)=-$\frac{3}{2}$,
所以$\frac{{t}^{2}}{2}$-t-3≥-$\frac{3}{2}$及t2-2t-3≥0,
解得t的取值范围为{t|t≤-3或t≥1}.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.

练习册系列答案
相关题目
2.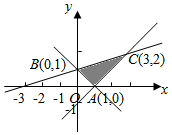 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
11.若a<b<0,则下列不等式成立的是( )
| A. | a2<b2 | B. | ab<b2 | C. | ab>a2 | D. | $a-\frac{1}{a}<b-\frac{1}{b}$ |
8.设an=-n2+9n+10,则数列{an}前n项和最大时n的值为( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 12 |
15.若实数a,b满足$\frac{1}{a^2}+\frac{1}{b^2}=ab$,则ab的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
 如图所示,四棱锥P-ABCD,平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点.
如图所示,四棱锥P-ABCD,平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点.