题目内容
14.已知$sin(π-α)=-\frac{1}{2}$,则sin(-2π-α)=$\frac{1}{2}$.分析 由已知利用诱导公式即可计算得解.
解答 解:∵$sin(π-α)=-\frac{1}{2}$,
∴sinα=-$\frac{1}{2}$,
∴sin(-2π-α)=-sin(2π+α)=-sinα=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
相关题目
5.已知向量$\overrightarrow a$表示“向东航行3km”,向量$\overrightarrow b$表示“向南航行3km,则$\overrightarrow a$+$\overrightarrow b$表示( )
| A. | 向东南航行6km | B. | 向东南航行3$\sqrt{2}$km | C. | 向东北航行3$\sqrt{2}$km | D. | 向东北航行6km |
9.等比数列1,a2,a3,$\frac{1}{8}$,…的前5项的和为( )
| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | $\frac{15}{8}$ | D. | $\frac{15}{16}$ |
19.已知扇形的弧长是4cm,面积是2cm2,则扇形的圆心角的弧度数是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 1或4 |
2.已知集合M,N⊆I,若M∩N=N,则( )
| A. | ∁IM?∁IN | B. | M⊆∁IN | C. | ∁IM⊆∁IN | D. | M?∁IN |
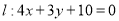 ,半径为
,半径为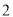 的圆
的圆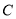 与
与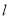 相切,圆心
相切,圆心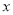 轴上且在直线
轴上且在直线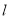 的右上方.
的右上方.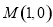 且与圆
且与圆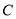 交于
交于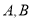 两点(
两点(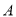 在
在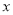 轴上方,B在
轴上方,B在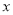 轴正半轴上是否存在定点
轴正半轴上是否存在定点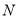 ,使得
,使得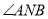 ?若存在,请求出点
?若存在,请求出点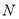 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.