题目内容
6.用数学归纳法证明:“1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{{{2^n}-1}}<n({n∈{N^*},n>1})$”由n=k(k∈N*,k>1)不等式成立,推理n=k+1时,不等式左边应增加的项数为2k.分析 分别计算当n=k和n=k+1时左侧最后一项的分母即左侧的项数即可得出答案.
解答 解:当n=k时,不等式左侧为1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$,
当n=k+1时,不等式左侧为1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$+$\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}-1}$
不等式左边增加的项数是(2k+1-1)-(2k-1)=2k.
故答案为:2k.
点评 本题考查数学归纳法,考查观察、推理与运算能力,属于中档题.

练习册系列答案
相关题目
17.已知集合U=R,Q={x|-2≤x≤3},P={x|x-2<0},则Q∩(∁UP)=( )
| A. | {x|1≤x≤2} | B. | {x|x≥1} | C. | {x|1<x≤2} | D. | {x|2≤x≤3} |
11.不等式|x+1|≥kx对任意的x∈R均成立,则k的取值范围是( )
| A. | (-∞,0) | B. | [-1,0] | C. | [0,1] | D. | [0,+∞) |
18.已知定义在R上的函数f(x)满足:①f(x)=f(4-x),②f(x+2)=f(x),③在[0,1]上表达式为f(x)=2x-1,则函数g(x)=f(x)-log3|x|的零点个数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
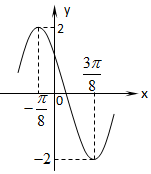 已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,
已知函数$f(x)=Asin(ωx+\frac{3π}{4})$(A>0,ω>0,|φ|<π)的一段图象如图所示,