题目内容
14.求函数$f(x)=2{sin^2}x+2\sqrt{3}sinx•cosx+1\;(x∈R)$的值域,最小正周期及单调递增区间.分析 利用二倍角以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;结合三角函数的图象和性质,求出f(x)的最大值和最小值,即得到f(x)的值域.
解答 解:函数$f(x)=2{sin^2}x+2\sqrt{3}sinx•cosx+1\;(x∈R)$.
化简可得:f(x)=1-cos2x+$\sqrt{3}$sin2x+1=$\sqrt{3}$sin2x-cos2x+2=2sin(2x-$\frac{π}{6}$)+2.
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
∵sin(2x-$\frac{π}{6}$)∈[-1,1],
∴函数f(x)的值域为[0,4].
令$-\frac{π}{2}+2kπ≤$2x-$\frac{π}{6}$$≤\frac{π}{2}+2kπ$,k∈Z.
得:$-\frac{π}{6}+kπ$≤x≤$\frac{π}{3}+kπ$,
∴函数f(x)的单调递增区间为[$-\frac{π}{6}+kπ$,$\frac{π}{3}+kπ$],k∈Z.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键,属于基础题.

练习册系列答案
相关题目
2.下列求导正确的是( )
| A. | (3x2-2)'=3x | B. | (log2x)'=$\frac{1}{x•ln2}$ | C. | (cosx)'=sinx | D. | ($\frac{1}{lnx}$)'=x |
19.命题“?x0∈R,$\frac{2}{x_0}$+lnx0≥0”的否定是( )
| A. | $?{x}∈R,\frac{2}{x}+ln{x}<0$ | B. | $?{x}∈R,\frac{2}{x}+ln{x}≤0$ | ||
| C. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}<0$ | D. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}≤0$ |
6.命题“?x∈R,x2+x+1<0”的否定为( )
| A. | ?x∈R,x2+x+1≥0 | B. | ?x∉R,x2+x+1≥0 | ||
| C. | ?x0∉R,x02+x0+1<0 | D. | ?x0∈R,x02+x0+1≥0 |
3.设等比数列{an}中,a3=3,a4=9,若a1•a2•a3•…•an=344,则n=( )
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
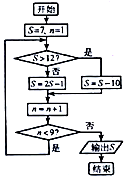 阅读如图的程序框图,运行相应的程序,则输出的S值为3.
阅读如图的程序框图,运行相应的程序,则输出的S值为3. 已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.