题目内容
4．
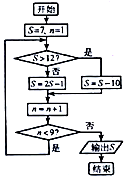阅读如图的程序框图，运行相应的程序，则输出的S值为3．
分析 由已知程序框图逐步判断、执行，知道满足n＜9不成立结束算法，输出S值．
解答 解：赋值S=7，n=1，
判断7＞12不成立，执行S=2×7-1=13，n=1+1=2，判断2＜9成立；
判断13＞12成立，执行S=13-10=3，n=2+1=3，判断3＜9成立；
判断3＞12不成立，执行S=2×3-1=5，n=3+1=4，判断4＜9成立；
判断5＞12不成立，执行S=2×5-1=9，n=4+1=5，判断5＜9成立；
判断9＞12不成立，执行S=2×9-1=17，n=5+1=6，判断6＜9成立；
判断17＞12成立，执行S=17-10=7，n=6+1=7，判断7＜9成立；
判断7＞12不成立，执行S=2×7-1=13，n=6+1=7，判断7＜9成立；
判断13＞12成立，执行S=13-10=3，n=8+1=9，判断9＜9不成立，算法结束，输出S=3．
故答案为：3．
点评 本题考查程序框图，考查学生读取图表的能力，是基础题．
练习册系列答案
相关题目
15．已知过抛物线x2=4y焦点F的直线交抛物线于A、B两点（点A在第一象限），若$\overrightarrow{AF}=3\overrightarrow{FB}$，则直线的方程为（ ）
| A． | $\sqrt{3}x-y-\sqrt{3}=0$ | B． | $x-\sqrt{3}y+\sqrt{3}=0$ | C． | $x-\sqrt{3}y-1=0$ | D． | $\sqrt{3}x-y+1=0$ |
15．已知数列{an+81}是公比为3的等比数列，其中a1=-78，则数列{|an|}的前100项和为（ ）
| A． | $\frac{{{3^{101}}-16203}}{2}$ | B． | $\frac{{{3^{100}}-15387}}{2}$ | C． | $\frac{{{3^{101}}-15387}}{2}$ | D． | $\frac{{{3^{100}}-16203}}{2}$ |
16．随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查50人，并将调查情况进行整理后制成如表：
（1）世界联合国卫生组织规定：[15，45）岁为青年，（45，60）为中年，根据以上统计数据填写以下2×2列联表：
（2）判断能否在犯错误的概率不超过0.05的前提下，认为赞成“车柄限行”与年龄有关？
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{a+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
独立检验临界值表：
（3）若从年龄[15，25），[25，35）的被调查中各随机选取1人进行调查，设选中的两人中持不赞成“车辆限行”态度的人员为ξ，求随机变量ξ的分布列和数学期望Eξ．
| 年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，60） |
| 频数 | 10 | 10 | 10 | 10 | 10 |
| 赞成人数 | 3 | 5 | 6 | 7 | 9 |
| 青年人 | 中年人 | 合计 | |
| 不赞成 | 16 | 4 | 20 |
| 赞成 | 14 | 16 | 30 |
| 合计 | 30 | 20 | 50 |
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{a+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
独立检验临界值表：
| P（K2≥k） | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |