题目内容

4．证明不等式：ex＞1+x（x≠0）．

分析 构造函数f（x）=ex-1-x，求出导函数，利用导函数求出函数的最小值，得出f（x）＞0，进而得出结论成立．

解答 证明：设函数f（x）=ex-1-x．
f'（x）=ex-1，
当x＞0时，f'（x）＞0，f（x）递增；
当x＜0时，f'（x）＜0，f（x）递减，
∴f（x）＞f（0）=0，
∴f（x）＞0，
∴ex＞1+x（x≠0）．

点评 本题考查了导函数的基本应用，和构造函数方法的应用，属于基础题型，应熟练掌握．

练习册系列答案
相关题目
14．求函数$f（x）=2{sin^2}x+2\sqrt{3}sinx•cosx+1\;（x∈R）$的值域，最小正周期及单调递增区间．
15．要得到函数y=cos（2x+$\frac{π}{3}$）的图象，只需将函数y=cos2x的图象（　　）
A．向左平行移动$\frac{π}{3}$个单位长度B．向右平行移动$\frac{π}{3}$个单位长度
C．向左平行移动$\frac{π}{6}$个单位长度D．向右平行移动$\frac{π}{6}$个单位长度
12．某校高一（1）、（2）两个班联合开展“诗词大会进校园，国学经典润心田”古诗词竞赛主题班会活动，主持人从这两个班分别随机选出20名同学进行当场测试，他们的测试成绩按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）分组，分组用频率分布直方图与茎叶统计如下（单位：分）
（1）班20名同学成绩频率分布直方图

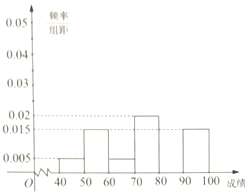
（2）班20名同学成绩茎叶图
45
52
64 5 6 8
70 5 5 8 8 8 8 9
8005 5
945
（Ⅰ）分別计算两个班这20名同学的测试成绩在[80，90）的频率，并补全频率分布直方图；
（Ⅱ）从（2）班参加测试的不低于80分的同学中随机选取两人，求这两人中至少有1人的成绩在90分以上的概率；
（III ）运用所学统计知识分析比较两个班学生的古诗词水平．
19．狄利克雷函数是高等数学中的一个典型函数，若f（x）=$\left\{\begin{array}{l}{1，x∈Q}\\{0，x∈{C}_{R}Q}\end{array}\right.$，则称f（x）为狄利克雷函数．对于狄利克雷函数f（x），给出下面4个命题：①对任意x∈R，都有f[f（x）]=1；②对任意x∈R，都有f（-x）+f（x）=0；③对任意x1∈R，都有x2∈Q，f（x1+x2 ）=f（x1）；④对任意a，b∈（-∞，0），都有{x|f（x）＞a}={x|f（x）＞b}．其中所有真命题的序号是（　　）
A．①④B．③④C．①②③D．①③④
9．已知数列{an}前n项和Sn=$\frac{3}{2}$n2-$\frac{123}{2}$n，n∈N*
（1）求数列{an}的通项公式an；
（2）求Tn=|a1|+|a2|+…+|an|的值．
16．已知函数f（x）=logax，g（x）=loga（2x+t-2），其中a＞0且a≠1，t∈R．
（1）若0＜a＜1，且x∈[$\frac{1}{4}$，2]时，有2f（x）≥g（x）恒成立，求实数t的取值范围；
（2）若t=4，且x∈[$\frac{1}{4}$，2]时，F（x）=2g（x）-f（x）的最小值是-2，求实数a的值．
13．已知$\frac{5i}{2-i}=a+bi$（a，b∈R，i为虚数单位），则a+b=1．
14．用“五点法”画y=2sin（2x+$\frac{π}{3}$）在一个周期内的简图时，所描的五个点分别是（$-\frac{π}{6}$，0），（$\frac{π}{12}$，2），（$\frac{π}{3}$，0），（$\frac{7π}{12}$，-2），（$\frac{5π}{6}$，0）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网