题目内容
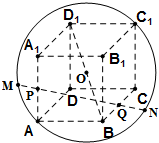 棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )
棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )A、
| ||
B、2
| ||
| C、3 | ||
D、
|
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:如图连接OP,OQ,OM,作OE⊥PQ,△OPQ为等腰三角形,求出OP,OE=d,求出球的半径,然后利用勾股定理,求出MN的长度即可.
解答:
解:连接OP,OQ,OM,作OE⊥PQ,如图,易知△OPQ为等腰三角形,|OP|=|OQ|=
,|PQ|=
=
,
可求得0到PQ的距离为d=
=
,
 球的半径为
球的半径为
×
=
.
MN的长为:2
=
.
故选:D.
| 2 |
| 12+22+12 |
| 6 |
可求得0到PQ的距离为d=
(
|
| ||
| 2 |
 球的半径为
球的半径为| 1 |
| 2 |
| 22+22+22 |
| 3 |
MN的长为:2
(
|
| 10 |
故选:D.
点评:本题考查学生作图能力,空间想象能力,计算能力,两次使用勾股定理,解题的关键在于理解题意.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线3x-4y=9的距离等于1,则半径r的范围是( )
| A、[3,5) |
| B、(3,5) |
| C、(3,5] |
| D、[3,5] |
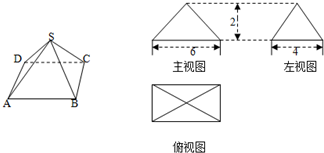
某台体的三视图如图所示,则该台体的体积是( )


A、(5+
| ||
| B、28π | ||
| C、7π | ||
| D、21π |
 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是( )| A、18 | ||
B、2
| ||
C、12+
| ||
D、18+2
|