题目内容
记关于x的不等式
＞1（a＞0）的解集为P，不等式|x-1|≤1的解集为Q．
（Ⅰ）若a=3，求集合P；
（Ⅱ）若Q∩P=Q，求实数a的取值范围．
| 1+a |
| x+1 |
（Ⅰ）若a=3，求集合P；
（Ⅱ）若Q∩P=Q，求实数a的取值范围．
考点：集合关系中的参数取值问题
专题：集合
分析：（1）通过解分式不等式求得集合P；
（2）解绝对值不等式求得集合Q，根据Q∩P=Q，得Q⊆P，由此求出a的取值范围．
（2）解绝对值不等式求得集合Q，根据Q∩P=Q，得Q⊆P，由此求出a的取值范围．
解答：
解：（1）当a=3时，由
＞1⇒
＜0⇒-1＜x＜3；
∴集合P={x|-1＜x＜3}；
（2）由|x-1|≤1⇒0≤x≤2．
∴Q={x|0≤x≤2}，
∵Q∩P=Q，
∴Q⊆P，
由
＞1⇒
＜0，
∴a＞2．
| 1+3 |
| x+1 |
| x-3 |
| x+1 |
∴集合P={x|-1＜x＜3}；
（2）由|x-1|≤1⇒0≤x≤2．
∴Q={x|0≤x≤2}，
∵Q∩P=Q，
∴Q⊆P，
由
| 1+a |
| x+1 |
| x-a |
| x+1 |
∴a＞2．
点评：本题考查了分式不等式与绝对值不等式的解法，考查了集合包含关系的应用，体现了数形结合思想．
练习册系列答案
相关题目
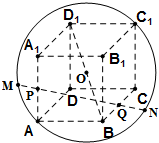棱长为2的正方体ABCD-A1B1C1D1内接于球O，则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为（ ）A、
| ||
B、2
| ||
| C、3 | ||
D、
|
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）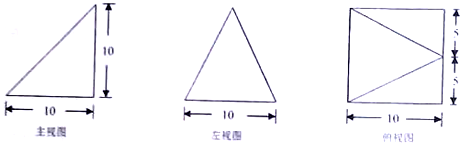
A、
| ||
B、
| ||
| C、1000cm3 | ||
| D、2000cm3 |
以（-1，2）为圆心，
为半径的圆的方程为（ ）
| 5 |
| A、x2+y2-2x+4y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2+2x-4y=0 |
| D、x2+y2-2x-4y=0 |