题目内容
已知正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
a,则AC1与侧面ABB1A1所成的角的正弦值等于 .
| 2 |
考点:直线与平面所成的角
专题:空间位置关系与距离
分析:取A1B1的中点E,由正三棱柱性质得面A1B1C1⊥面A1B1BA,从面推导出∠C1AE为AC1与侧面ABB1A1所成的角,由此能求出结果.
解答:
解:如图,取A1B1的中点E,连结C1E,AE,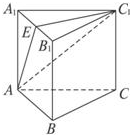
由正三棱柱性质得面A1B1C1⊥面A1B1BA,交线是A1B1.
又C1E⊥A1B1,∴C1E⊥面A1B1BA.
∴∠C1AE为所求.
∵AB=a,C1C=
a,
∴Rt△C1EA中,C1E=
,AE=
a.
∴tan∠C1AE=
=
.∴∠C1AE=30°.
∴AC1与面ABB1A1所成的角为30°.
∴AC1与侧面ABB1A1所成的角的正弦值为sin30°=
.
故答案为:
.

由正三棱柱性质得面A1B1C1⊥面A1B1BA,交线是A1B1.
又C1E⊥A1B1,∴C1E⊥面A1B1BA.
∴∠C1AE为所求.
∵AB=a,C1C=
| 2 |
∴Rt△C1EA中,C1E=
| ||
| 2 |
| 3 |
| 2 |
∴tan∠C1AE=
| C1E |
| AE |
| ||
| 3 |
∴AC1与面ABB1A1所成的角为30°.
∴AC1与侧面ABB1A1所成的角的正弦值为sin30°=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在集合S={1,2,3,…,30}的12元子集T={a1,a2…,a12}中,恰有两个元素的差的绝对值等于1,这样的12元子集T的个数为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知a,b∈R且a>b,则下列不等式中成立的是( )
A、
| ||
| B、a2>b2 | ||
| C、ln(a-b)>0 | ||
| D、2a-b>1 |
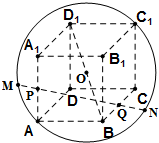 棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )
棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )A、
| ||
B、2
| ||
| C、3 | ||
D、
|