题目内容
已知函数f(x)=kx+b的图象过点(2,1)且方向向量
=(1,-1),若不等式f(x)≥x2+x-5
的解集为A⊆(-∞,a]
(1)求a的取值范围;
(2)解不等式
<1.
| ν |
的解集为A⊆(-∞,a]
(1)求a的取值范围;
(2)解不等式
| x2-(a+3)x+2a+3 |
| f(x) |
考点:其他不等式的解法,一次函数的性质与图象
专题:不等式的解法及应用
分析:(1)由题意可得
,可得 f(x)的解析式.由 f(x)≥x2+x-5求得A=[-4,2].再根据[-4,2]⊆(-∞,a],可得a的范围.
(2)不等式即(x-a)(x-2)(x-3)>0,由(1)知 a≥2.再分当a=2、2<a<3、a=3、a>3四种情况,分别求得不等式的解集.
|
(2)不等式即(x-a)(x-2)(x-3)>0,由(1)知 a≥2.再分当a=2、2<a<3、a=3、a>3四种情况,分别求得不等式的解集.
解答:
解:(1)∵函数f(x)=kx+b的图象过点(2,1)且方向向量
=(1,-1),
∴
⇒
,
∴f(x)=-x+3.
∴由 f(x)≥x2+x-5⇒x2+2x-8≤0,
∴A=[-4,2].
又[-4,2]⊆(-∞,a],∴a≥2.
(2)
<1⇒
<1⇒
>0⇒(x-a)(x-2)(x-3)>0,
由(1)知 a≥2.
当a=2时,不等式的解集为(3,+∞);
当2<a<3时,不等式的解集为(2,a)∪(3,+∞);
当a=3时,不等式的解集为(2,3)∪(3,+∞);
当a>3时,不等式的解集为(2,3)∪(a,+∞).
| ν |
∴
|
|
∴f(x)=-x+3.
∴由 f(x)≥x2+x-5⇒x2+2x-8≤0,
∴A=[-4,2].
又[-4,2]⊆(-∞,a],∴a≥2.
(2)
| x2-(a+3)x+2a+3 |
| f(x) |
| x2-(a+3)x+2a+3 |
| -x+3 |
| x2-(a+2)x+2a |
| x-3 |
由(1)知 a≥2.
当a=2时,不等式的解集为(3,+∞);
当2<a<3时,不等式的解集为(2,a)∪(3,+∞);
当a=3时,不等式的解集为(2,3)∪(3,+∞);
当a>3时,不等式的解集为(2,3)∪(a,+∞).
点评:本题主要考查一次函数的性质,分式不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
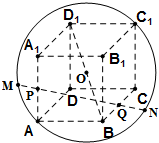 棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )
棱长为2的正方体ABCD-A1B1C1D1内接于球O,则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为( )A、
| ||
B、2
| ||
| C、3 | ||
D、
|
以(-1,2)为圆心,
为半径的圆的方程为( )
| 5 |
| A、x2+y2-2x+4y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2+2x-4y=0 |
| D、x2+y2-2x-4y=0 |
下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数为( )
| A、f(x)=x-1 | ||
| B、f(x)=cosx | ||
| C、f(x)=2|x| | ||
D、f(x)=log
|