题目内容
若圆（x-3）2+（y+5）2=r2上有且只有两个点到直线3x-4y=9的距离等于1，则半径r的范围是（ ）
| A、[3，5） |
| B、（3，5） |
| C、（3，5] |
| D、[3，5] |
考点：直线与圆相交的性质
专题：直线与圆
分析：由圆的标准方程找出圆心的坐标，利用点到直线的距离公式求出圆心到已知直线的距离d，由题意得到|d-r|小于1，将d的值代入得到关于r的不等式，求出不等式的解集即可得到圆半径r的取值范围．
解答：
解：由（x-3）2+（y+5）2=r2得，圆心坐标（3，-5），
∴圆心到直线3x-4y=9的距离d=
=4，
∴由题意得：|d-r|=|4-r|＜1，
解得3＜r＜5，
故选B．
∴圆心到直线3x-4y=9的距离d=
| |3×3+4×5-9| | ||
|
∴由题意得：|d-r|=|4-r|＜1，
解得3＜r＜5，
故选B．
点评：本题考查了直线与圆的位置关系，涉及的知识有：点到直线的距离公式，以及绝对值不等式的解法，其中根据题意得出|d-r|＜1（d为圆心到已知直线的距离）是解本题的关键．
练习册系列答案
相关题目
下列可能是三进制数的是（ ）
| A、2012 | B、2013 |
| C、2014 | D、2015 |
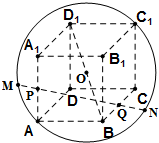棱长为2的正方体ABCD-A1B1C1D1内接于球O，则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为（ ）A、
| ||
B、2
| ||
| C、3 | ||
D、
|
圆x2+y2=2截直线x-y-1=0所得弦长为（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|