题目内容
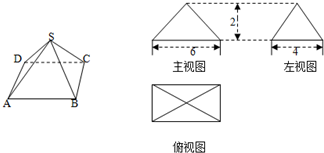
（文）四棱锥S-ABCD的底面是矩形，顶点S在底面的射影是矩形对角线的交点，且四棱锥及其三视图如图（AB平行于主视图投影平面），则四棱锥S-ABCD的体积为 ．
考点：由三视图求面积、体积
专题：计算题
分析：由三视图知四棱锥的底面矩形的长、宽分别为6、4，四棱锥的高为2，代入棱锥的体积公式计算可得答案．
解答：
解：由三视图知四棱锥的底面矩形的长、宽分别为6、4，四棱锥的高为2，
∴四棱锥的体积V=
×6×4×2=16．
故答案是16．
∴四棱锥的体积V=
| 1 |
| 3 |
故答案是16．
点评：本题考查了由三视图求几何体的体积，解答的关键是判断几何体的形状及三视图的数据所对应的几何量．
练习册系列答案
相关题目
若x2+y2=100，则直线4x-3y+50=0与圆的位置关系是（ ）
| A、相交 | B、相离 |
| C、相切 | D、相交但不过圆心 |
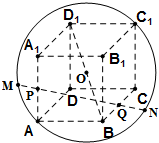棱长为2的正方体ABCD-A1B1C1D1内接于球O，则过棱AA1和BC的中点P、Q的直线被球面截得的弦MN的长为（ ）A、
| ||
B、2
| ||
| C、3 | ||
D、
|
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）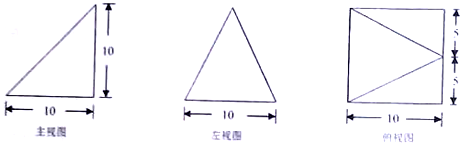
A、
| ||
B、
| ||
| C、1000cm3 | ||
| D、2000cm3 |