Question

12．$\int_0^2{[{x^2}+\sqrt{1-{{（x-1）}^2}}]dx=}$$\frac{8}{3}+\frac{π}{2}$．

Answer 1

分析 利用定积分的运算性质及定积分的几何意义，分别求得${∫}_{0}^{2}$x²dx和${∫}_{0}^{2}$$\sqrt{1-（x-1）^{2}}$dx的值．

解答 解：由$\int_0^2{[{x^2}+\sqrt{1-{{（x-1）}^2}}]dx=}$=${∫}_{0}^{2}$x²dx+${∫}_{0}^{2}$$\sqrt{1-（x-1）^{2}}$dx，
由${∫}_{0}^{2}$x²dx=$\frac{1}{3}$x³${丨}_{0}^{2}$=$\frac{8}{3}$，
由定积分的几何意义可知：${∫}_{0}^{2}$$\sqrt{1-（x-1）^{2}}$dx表示以（1，0）为圆心以1为半径的圆的一半，
则${∫}_{0}^{2}$$\sqrt{1-（x-1）^{2}}$dx=$\frac{π}{2}$，
$\int_0^2{[{x^2}+\sqrt{1-{{（x-1）}^2}}]dx=}$=${∫}_{0}^{2}$x²dx+${∫}_{0}^{2}$$\sqrt{1-（x-1）^{2}}$dx=$\frac{8}{3}+\frac{π}{2}$，
故答案为：$\frac{8}{3}+\frac{π}{2}$．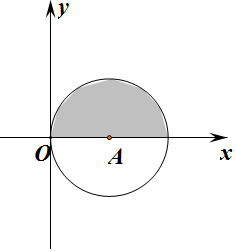

点评 本题考查定积分的运算，定积分的几何意义，考查计算能力，属于基础题．