题目内容
2.已知角α的终边过点P(1,-3),(Ⅰ)求sinα,cosα,tanα的值
(Ⅱ)求$\frac{sinα}{{cosα\sqrt{1+{{tan}^2}α}}}$的值.
分析 (Ⅰ)利用任意角的三角函数的定义,求得sinα,cosα,tanα的值
(Ⅱ)把tanα的值代入要求式子化简可的结果.
解答 解:(Ⅰ)∵角α的终边过点P(1,-3),∴x=1,y=-3,r=|OP|=$\sqrt{10}$,
∴sinα=$\frac{y}{r}$=-$\frac{3}{\sqrt{10}}$=-$\frac{3\sqrt{10}}{10}$,cosα=$\frac{x}{r}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$,tanα=$\frac{y}{x}$=-3.
(Ⅱ)由(Ⅰ)可得$\frac{sinα}{{cosα\sqrt{1+{{tan}^2}α}}}$=$\frac{tanα}{\sqrt{{1+tan}^{2}α}}$=$\frac{-3}{\sqrt{1+9}}$=-$\frac{3\sqrt{10}}{10}$.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
13.运行如图所示的程序框图,则输出结果为( )
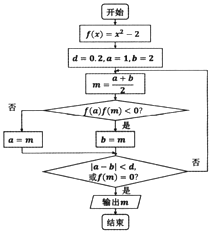

| A. | $\frac{11}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{23}{16}$ |
17.一年二十四班某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)某一个周期内的图象时,列表并填入了部分数据如表:
(1)请将上表数据补充完整,并写出函数f(x)解析式
(2)求f(x)最小正周期及单调增区间?
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | $\frac{13π}{12}$ | |
| Asin(ωx+φ) | 0 | 5 | 0 | -5 | 0 |
(2)求f(x)最小正周期及单调增区间?
11.若${(x-2)^5}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}$,则a1+a2+a3+a4+a5=( )
| A. | -1 | B. | -31 | C. | -33 | D. | 31 |
12.在△ABC中,内角A,B,C所对的边分别是a,b,c,若c2=(a-b)2+6,C=$\frac{π}{3}$,则△ABC的面积是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{9\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |