题目内容
1.(1)求值sin2120°+cos180°+tan45°-cos2(-330°)+sin(-210°)(2)已知$sin(π+α)=\frac{1}{2}(π<α<\frac{3π}{2})$,求sinα-cosα的值.
分析 (1)利用特殊角的三角函数值以及三角函数的诱导公式化简求值即可.
(2)利用同角三角函数基本关系式以及角的范围化简求值即可.
解答 解:(1)原式=($\frac{\sqrt{3}}{2}$)2-1+1-cos230°-sin210°
=$\frac{3}{4}$-($\frac{\sqrt{3}}{2}$)2+sin30°=sin30°=$\frac{1}{2}$.
(2)∵$sin(π+α)=-sinα=\frac{1}{2}$即$sinα=-\frac{1}{2}$.
∴${cos^2}α=1-{({-\frac{1}{2}})^2}=\frac{3}{4}$.
又∵$π<α<\frac{3π}{2}$,
∴$cosα=-\frac{{\sqrt{3}}}{2}$.
∴$sinα-cosα=-\frac{1}{2}+\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}-1}}{2}$.
点评 本题考查了三角函数的化简求值,考查了三角函数的诱导公式的运用,考查了同角三角函数基本关系式,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
13.运行如图所示的程序框图,则输出结果为( )
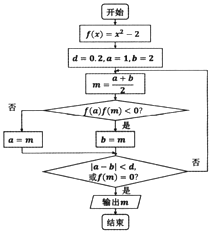

| A. | $\frac{11}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{23}{16}$ |