题目内容
6.在n行n列矩阵$|\begin{array}{l}{1}&{2}&{3}&{…}&{n-2}&{n-1}&{n}\\{2}&{3}&{4}&{…}&{n-1}&{n}&{1}\\{3}&{4}&{5}&{…}&{n}&{1}&{2}\\{…}&{…}&{…}&{…}&{…}&{…}&{…}\\{n}&{1}&{2}&{…}&{n-3}&{n-2}&{n-1}\end{array}|$中,记位于第i行j列的数为aij(i,j=1,2,…,n),当n=7时,表中所有满足2i<j的aij和为41.分析 根据题意n=7时,求得所有满足2i<j的aij,相加即可求得答案.
解答 解:由题意可知:当i=1时,由2i<j,
∴j取3,4,5,6,7,
当i=2时,j取5,6,7,
当i=3时,j取7,
∴表中所有满足2i<j的aij和为:
a13+a14+a15+a16+a17+a25+a26+a27+a37=3+4+5+6+7+6+7+1+2=41,
故答案为:41.
点评 本题考查高阶矩阵,考查学生的理解问题,分析解决问题的能力,考查aij中i和j的字母含义,属于中档题.

练习册系列答案
相关题目
17.定义在(0,+∞)上的可导函数f(x)满足:当x∈(0,e)时f(x)+xf′(x)>$\frac{1}{e}$当x∈(e,+∞)时f(x)+xf′(x)<$\frac{1}{e}$则下列对于2f(2),3f(3)大小关系的结论成立的是( )
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |
14.已知如图所示的程序框图,当输入n=99时,输出S的值( )
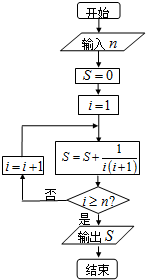

| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
18.仔细观察下面○和●的排列规律:○●○○●○○○●○○○○●○○○○○●○○○○○○●…
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
16.已知a=($\sqrt{2}$)-1,b=log23,c=lne,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.