题目内容

17．定义在（0，+∞）上的可导函数f（x）满足：当x∈（0，e）时f（x）+xf′（x）＞$\frac{1}{e}$当x∈（e，+∞）时f（x）+xf′（x）＜$\frac{1}{e}$则下列对于2f（2），3f（3）大小关系的结论成立的是（　　）
A．2f（2）＞3f（3）B．2f（2）＜3f（3）C．2f（2）=3f（3）D．无法确定

分析 构造函数g（x）=xf（x）-$\frac{1}{e}$x，（x＞0），求出函数的单调性，得到g（2）＜g（3），从而求出结论．

解答 解：令g（x）=xf（x）-$\frac{1}{e}$x，（x＞0），
当x∈（0，e）时f（x）+xf′（x）＞$\frac{1}{e}$，
当x∈（e，+∞）时f（x）+xf′（x）＜$\frac{1}{e}$，
故g（x）在（0，e）递增，在（e，+∞）递减，
∴g（2）＜g（3），
∴2f（2）-$\frac{2}{e}$＜3f（3）-$\frac{3}{e}$，
∴2f（2）＜3（3）-$\frac{1}{e}$＜3f（3），
故选：B．

点评 本题考查了函数的单调性问题，考查导数的应用，构造函数g（x）是解题的关键，本题是一道中档题．

练习册系列答案
相关题目
7．已知函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{2}\sqrt{{x^2}+1}，x≥0}\\{-ln（1-x），x＜0}\end{array}}$，若函数F（x）=f（x）-kx有且只有两个零点，则k的取值范围为（$\frac{1}{2}$，1）．
8．方程16x-17×22x+16=0的解是x=0，x=2．
5．若直线l的一般式方程为xsinθ-$\sqrt{3}$y+1=0（θ∈R），则直线l的倾斜角的取值范围是$[0，\frac{π}{6}]∪[\frac{5π}{6}，π）$．
12．使不等式x2＞x${\;}^{\frac{1}{2}}$成立的x的取值范围是（　　）
A．x＞1B．0＜x＜1C．x＞0D．x＜1
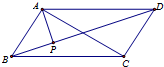2．如图，在平行四边形ABCD中，AP⊥BD，垂足为P，且AP=2，则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8．
9．已知数列{an}满足：a1=3，an+1=9•$\root{3}{{a}_{n}}$（n≥1），则$\underset{lim}{n→∞}$an=27．
6．在n行n列矩阵$|\begin{array}{l}{1}&{2}&{3}&{…}&{n-2}&{n-1}&{n}\\{2}&{3}&{4}&{…}&{n-1}&{n}&{1}\\{3}&{4}&{5}&{…}&{n}&{1}&{2}\\{…}&{…}&{…}&{…}&{…}&{…}&{…}\\{n}&{1}&{2}&{…}&{n-3}&{n-2}&{n-1}\end{array}|$中，记位于第i行j列的数为aij（i，j=1，2，…，n），当n=7时，表中所有满足2i＜j的aij和为41．
7．设函数f（x）=$\left\{{\begin{array}{l}{1+{{log}_2}（{2-x}），x＜1}\\{{2^{x-1}}，x≥1}\end{array}}$，则f（-6）+f（log212）=（　　）
A．10B．6C．9D．12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网