如图.已知直三棱柱ABC-A1B1C1中.∠ACB=90°.点D是AB的中点．(1)求证:AC⊥BC1,(2)求证:AC1∥平面CDB1．题目和参考答案——青夏教育精英家教网——

题目内容

1．

如图，已知直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，点D是AB的中点．
（1）求证：AC⊥BC₁；
（2）求证：AC₁∥平面CDB₁．

分析（1）由AC⊥BC，且BC₁在平面ABC内的射影为BC，能证明AC⊥BC₁．
（2）设CB₁与C₁B的交点为E，连结DE，由已知推导出DE∥AC₁，由此能证明AC₁∥平面CDB₁．

解答证明：（1）直三棱柱ABC-A₁B₁C₁，∠ACB=90°，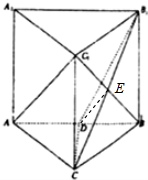
∴AC⊥BC，且BC₁在平面ABC内的射影为BC，
∴AC⊥BC₁．
（2）设CB₁与C₁B的交点为E，连结DE，
∵D是AB的中点，E是BC₁的中点，
∴DE∥AC₁，∵DE?平面CDB₁，AC₁?平面CDB₁，
∴AC₁∥平面CDB₁．

点评本题考查线线垂直、线面平行的证明，考查学生分析解决问题的能力，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案

重难点手册系列答案

创维新课堂系列答案

世纪百通主体课堂小学课时同步达标系列答案

世纪百通优练测系列答案

世纪百通课时作业系列答案

百分学生作业本题练王系列答案

小学1课3练培优作业本系列答案

中华题王系列答案

优翼学练优系列答案

优加学习方案系列答案

相关题目

11．设$\overrightarrow{a}$，$\overrightarrow{b}$是不共线的两个非零向量．
（1）若$\overrightarrow{OA}$=2$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{OB}$=3$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{a}$-3$\overrightarrow{b}$，求证：A、B、C三点共线；
（2）设$\overrightarrow{OM}$=m$\overrightarrow{a}$，$\overrightarrow{ON}$=n$\overrightarrow{b}$，$\overrightarrow{OP}$=α$\overrightarrow{a}$+β$\overrightarrow{b}$，其中m，n，α，β均为实数，m≠0，n≠0，若M、P、N三点共线，求证：$\frac{α}{m}$+$\frac{β}{n}$=1．

12．使不等式x²＞x${\;}^{\frac{1}{2}}$成立的x的取值范围是（　　）

9．已知数列{a_n}满足：a₁=3，a_n+1=9•$\root{3}{{a}_{n}}$（n≥1），则$\underset{lim}{n→∞}$a_n=27．

16．已知a，b为直线，α，β，γ为平面，有下列命题中正确的是（　　）

a∥α，b∥β，则a∥b

a⊥γ，b⊥γ，则a∥b

a∥b，b?α，则a∥α

a⊥b，a⊥α，则b∥α

6．在n行n列矩阵$|\begin{array}{l}{1}&{2}&{3}&{…}&{n-2}&{n-1}&{n}\\{2}&{3}&{4}&{…}&{n-1}&{n}&{1}\\{3}&{4}&{5}&{…}&{n}&{1}&{2}\\{…}&{…}&{…}&{…}&{…}&{…}&{…}\\{n}&{1}&{2}&{…}&{n-3}&{n-2}&{n-1}\end{array}|$中，记位于第i行j列的数为a_ij（i，j=1，2，…，n），当n=7时，表中所有满足2i＜j的a_ij和为41．

13．已知函数f（x）=sin（2x-$\frac{π}{6}$）+sin（2x+$\frac{π}{6}$）+2cos²x+a-1（a∈R，a是常数）．
（1）求函数的最小正周期；
（2）求函数的单调递减区间；
（3）若x∈[0，$\frac{π}{2}$]时，f（x）的最小值为-2，求a的值．

10．袋子中装有大小相同的5个小球，分别有 2个红球，3个白球．现从中随机抽取2个小球，则这2个球中既有红球也有白球的概率为$\frac{3}{5}$．

11．有一休闲广场东侧建造一座钟楼，顶部嵌入一座大型时钟，钟面中心O距离地面30米，时钟分钟OP（P为分针末端）长8米，该挂钟于6月1日0点分开始揭幕启动．记经过t分钟时P距离地面的高度为h（t）米．
（Ⅰ）求h（t）的函数解析式；
（Ⅱ）求启动后1小时内，h=26，t为何值．