题目内容
一次函数y=kx+b与y=2x+1平行，且经过点（-3，4），则表达式为： ．
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：由已知得k=2，又y=2x+b经过点（-3，4），由此能求出该一次函数的表达式．
解答：
解：∵一次函数y=kx+b与y=2x+1平行，
∴k=2，即y=2x+b，
∵y=2x+b经过点（-3，4），
∴4=-6+b，解得b=10，
∴该一次函数为：y=2x+10．
故答案为：y=2x+10．
∴k=2，即y=2x+b，
∵y=2x+b经过点（-3，4），
∴4=-6+b，解得b=10，
∴该一次函数为：y=2x+10．
故答案为：y=2x+10．
点评：本题考查一次函数的表达式的求法，是基础题，解题时要注意两个一次函数平行的性质的合理运用．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
已知函数f（x）在R上可导，其导函数为f′（x），且函数F（x）=（1-x）f′（x）的图象如图所示，零点分别为-1，1，2，则f（-1），f（1），f（2）的大小关系正确的是（ ）| A、f（-1）=f（1）=f（2） |
| B、f（-1）＜f（1）＜f（2） |
| C、f（-1）＞f（1）＞f（2） |
| D、f（-1）＜f（2）＜f（1） |
已知一次函数y=kx+b的图象如图所示，则k，b的符号是（ ）
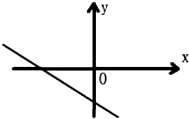
| A、k＞0，b＞0 |
| B、k＞0，b＜0 |
| C、k＜0，b＞0 |
| D、k＜0，b＜0 |
设U={1，2，3，4，5}，若A∩B={2}，（∁UA）∩B={4}，（∁UA）∩（∁UB）={1，5}，则下列结论正确的是（ ）
| A、3∉A且3∉B |
| B、3∈A且3∉B |
| C、3∉A且3∈B |
| D、3∈A且3∈B |