题目内容
设函数f(x)=
-ax,若曲线y=f(x)在点(e,f(e))处的切线斜率为2.
(Ⅰ)求a的值;
(Ⅱ)求f(x)在(1,+∞)上的单调区间与极值.
| x |
| lnx |
(Ⅰ)求a的值;
(Ⅱ)求f(x)在(1,+∞)上的单调区间与极值.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,导数的综合应用
分析:(Ⅰ)求出函数的导数,由切线的斜率为2,得到a的方程,即可求得a;
(Ⅱ)求出函数f(x)的导数,根据x>1,令导数大于0,得到增区间,令导数小于0,得到减区间,
从而得到函数的极小值,无极大值.
(Ⅱ)求出函数f(x)的导数,根据x>1,令导数大于0,得到增区间,令导数小于0,得到减区间,
从而得到函数的极小值,无极大值.
解答:
解:(Ⅰ)f′(x)=
-a⇒f′(e)=-a=2⇒a=-2
(Ⅱ)f′(x)=
+2=
=
≥0⇒x≥
则函数f(x)的单调递增区间为(
,+∞),
令f′(x)<0,得1<x<
,
单调递减区间为(1,
);
则f(x)在x=
处取极小值f(
)=4
,无极大值.
| lnx-1 |
| (lnx)2 |
(Ⅱ)f′(x)=
| lnx-1 |
| (lnx)2 |
| 2(lnx)2+lnx-1 |
| (lnx)2 |
| (2lnx-1)(lnx+1) |
| (lnx)2 |
| e |
则函数f(x)的单调递增区间为(
| e |
令f′(x)<0,得1<x<
| e |
单调递减区间为(1,
| e |
则f(x)在x=
| e |
| e |
| e |
点评:本题考查导数的几何意义,考查导数的运用:求单调区间和极值,考查运算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
下列命题正确的是( )
①任何一个函数的定义域皆非空.
②直线x=a与函数f(x)图象有且仅有一个公共点.
③
表示5的n次方根.
④若函数f(x)没有最大值,则f(x)一定趋近于+∞.
⑤若函数f(x)在[-1,0]单调递增且在[0,1]单调递增,则函数f(x)在[-1,1]一定单调递增.
①任何一个函数的定义域皆非空.
②直线x=a与函数f(x)图象有且仅有一个公共点.
③
| n | 5n |
④若函数f(x)没有最大值,则f(x)一定趋近于+∞.
⑤若函数f(x)在[-1,0]单调递增且在[0,1]单调递增,则函数f(x)在[-1,1]一定单调递增.
| A、①⑤ | B、①③⑤ |
| C、①②③④ | D、①②④⑤ |
运行如图所示的流程图,则输出的结果an是( )


| A、1 | B、-1 | C、-4 | D、-5 |
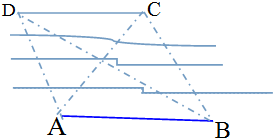 如图所示,为了测量河对岸两个建筑物C,D两点之间的距离,在河岸这边选取点A,B,测得∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,又已知AB=
如图所示,为了测量河对岸两个建筑物C,D两点之间的距离,在河岸这边选取点A,B,测得∠BAC=45°,∠DAC=75°,∠ABD=30°,∠DBC=45°,又已知AB=