题目内容
为了解某班关注NBA(美国职业篮球)是否与性别有关,对某班48人进行了问卷调查得到如下的列联表:
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为
.
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由;
(2)设甲,乙是不关注NBA的6名男生中的两人,丙,丁,戊是关注NBA的10名女生中的3人,从这5人中选取2人进行调查,求:甲,乙至少有一人被选中的概率.
答题参考:
K2=
,n=a+b+c+d.
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
| 2 |
| 3 |
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由;
(2)设甲,乙是不关注NBA的6名男生中的两人,丙,丁,戊是关注NBA的10名女生中的3人,从这5人中选取2人进行调查,求:甲,乙至少有一人被选中的概率.
答题参考:
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验
专题:计算题,概率与统计
分析:(1)利用列联表计算相关指数K2的观测值,比较临界值表,可得关注NBA与性别有关判断的可靠性程度;
(2)利用排列组合计算从5人中选2人的基本事件数和甲、乙至少有一人被选中的基本事件数,利用古典概型概率公式计算.
(2)利用排列组合计算从5人中选2人的基本事件数和甲、乙至少有一人被选中的基本事件数,利用古典概型概率公式计算.
解答:
解:(1)列联表补充如下:
由公式K2=
≈4.286,
∵4.286>3.841.故有95%把握认为关注NBA与性别有关:
(2)从5人中选2人的基本事件有:
=10,共10种,
其中甲、乙至少有一人被选中有
-
=7:共7种,
∴所求的概率为P=
.
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
| 48×(220-60)2 |
| 28×20×32×16 |
∵4.286>3.841.故有95%把握认为关注NBA与性别有关:
(2)从5人中选2人的基本事件有:
| C | 2 5 |
其中甲、乙至少有一人被选中有
| C | 2 5 |
| C | 2 3 |
∴所求的概率为P=
| 7 |
| 10 |
点评:本题考查了独立性检验及排列组合的应用,考查了古典概型的概率计算,熟练掌握独立性检验的思想方法是解题的关键.

练习册系列答案
相关题目
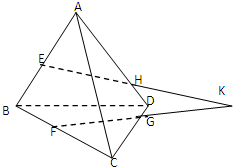 如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证:
如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证: