题目内容
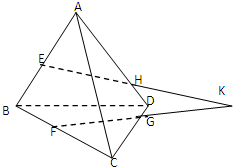 如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证:
如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证:(1)EH,BD,FG三条直线相交于同一点K;
(2)EF∥HG.
考点:平面的基本性质及推论,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)先证P为两个平面的公共点,利用两个平面的公共点在两个平面的公共直线上,证线共点;
(2)证明EF∥平面ACD,E,F,G,H,K共面于平面EFK,即可得证.
(2)证明EF∥平面ACD,E,F,G,H,K共面于平面EFK,即可得证.
解答:
 证明:(1)∵E、H分别是棱AB、AD上的点,
证明:(1)∵E、H分别是棱AB、AD上的点,
∴EH?平面ABD-------1’
又∵EH∩FG=K,∴K∈EH,即K∈平面ABD-------2’
同理可证,K∈平面BCD--------3’
∵平面ABD∩平面BCD=BD∴K∈BD-----4’
即EH,BD,FG三条直线相交于同一点K.---------5’
(2)连接EF,HG(如图),
∵在△ABC中,E,F分别是棱AB,BC的中点,
∴EF∥AC--------6’
∵EF?平面ACD,-----7’
∴EF∥平面ACD-----8’
又∵H,G分别是棱AD,CD的点,且EH∩FG=K,
∴E,F,G,H,K共面于平面EFK,
且平面EFK∩平面ACD=HG-------9’
故EF∥HG------10’
 证明:(1)∵E、H分别是棱AB、AD上的点,
证明:(1)∵E、H分别是棱AB、AD上的点,∴EH?平面ABD-------1’
又∵EH∩FG=K,∴K∈EH,即K∈平面ABD-------2’
同理可证,K∈平面BCD--------3’
∵平面ABD∩平面BCD=BD∴K∈BD-----4’
即EH,BD,FG三条直线相交于同一点K.---------5’
(2)连接EF,HG(如图),
∵在△ABC中,E,F分别是棱AB,BC的中点,
∴EF∥AC--------6’
∵EF?平面ACD,-----7’
∴EF∥平面ACD-----8’
又∵H,G分别是棱AD,CD的点,且EH∩FG=K,
∴E,F,G,H,K共面于平面EFK,
且平面EFK∩平面ACD=HG-------9’
故EF∥HG------10’
点评:本题考查了用公理2证明点共线问题,考查平行关系的转化,考查了学生的空间想象能力和推理论证能力,本题较好的体现了线线、线面平行关系的转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.
已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.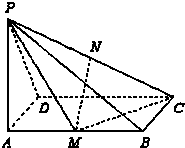 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1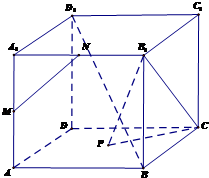 如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,
如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,