��Ŀ����
�Ķ�������ϣ��������Ǻ��������ҹ�ʽ����
sin����+�£�=sin��cos��+cos��sin�� ����
sin����-�£�=sin��cos��-cos��sin�� ����
�ɢ�+�ڵ�sin����+�£�+sin����-�£�=2sin��cos�� ����
���+��=A����-��=B ��=
����=
����۵�sinA+sinB=2sin
cos
��
��1�������������ۣ�����sin15��+sin75���ֵ��
��2�����������֤�������������Ǻ��������ҹ�ʽ��֤����cosA+cosB=2cos
•cos
��
��3������y=cos2x•cos��2x+
��x��[0��
]�����ֵ��
sin����+�£�=sin��cos��+cos��sin�� ����
sin����-�£�=sin��cos��-cos��sin�� ����
�ɢ�+�ڵ�sin����+�£�+sin����-�£�=2sin��cos�� ����
���+��=A����-��=B ��=
| A+B |
| 2 |
| A-B |
| 2 |
����۵�sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
��1�������������ۣ�����sin15��+sin75���ֵ��
��2�����������֤�������������Ǻ��������ҹ�ʽ��֤����cosA+cosB=2cos
| A+B |
| 2 |
| A-B |
| 2 |
��3������y=cos2x•cos��2x+
| �� |
| 6 |
| �� |
| 4 |
���㣺�������,���Ǻ��������Һ���
ר�⣺������,���Ǻ�������ֵ,���Ǻ�����ͼ��������
��������1����sinA+sinB=2sin
cos
����A=15�㣬B=75�㣬���Ϳɵ�sin15��+sin75���ֵ��
��2����cos����+�£�=cos��cos��-sin��sin�£�cos����-�£�=cos��cos��+sin��sin����ʽ��ӵã�cos����+�£�+cos����-�£�=2cos��cos�£����+��=A����-��=B �Ц�=
����=
���ɵý��ۣ�
��3����ϣ�2���Ľ��ۣ���A=2x��B=2x+
�����뻯�����Ľ���ʽ����������x��[0��
]��������4x+
��[
��
]�������������Һ�����ͼ������ʵõ�����y=cos2x•cos��2x+
��x��[0��
]�����ֵ��
| A+B |
| 2 |
| A-B |
| 2 |
��2����cos����+�£�=cos��cos��-sin��sin�£�cos����-�£�=cos��cos��+sin��sin����ʽ��ӵã�cos����+�£�+cos����-�£�=2cos��cos�£����+��=A����-��=B �Ц�=
| A+B |
| 2 |
| A-B |
| 2 |
��3����ϣ�2���Ľ��ۣ���A=2x��B=2x+
| �� |
| 6 |
| �� |
| 4 |
| �� |
| 6 |
| �� |
| 6 |
| 7�� |
| 6 |
| �� |
| 6 |
| �� |
| 4 |
���
�⣺��1����sinA+sinB=2sin
cos
��sin15��+cos75��=2sin
•cos
=2sin45��•cos��-30�㣩=
��3
��2����Ϊcos����+�£�=cos��cos��-sin��sin�£�------��
cos����-�£�=cos��cos��+sin��sin��------�ڡ�5
��+�ڵ�cos����+�£�+cos����-�£�=2cos��cos�£���
���+��=A����-��=B ��=
����=
����6
����۵ã�cosA+cosB=2cos
•cos
����7
��3���ɣ�2��֪��y=cos2xcos(2x+
)=
[cos(4x+
)+cos
]=
cos(4x+
)+
��8
��x��[0��
]��
��4x+
��[
��
]����..9
�ʺ��������ֵΪf(0)=
����10
| A+B |
| 2 |
| A-B |
| 2 |
��sin15��+cos75��=2sin
| 15��+75�� |
| 2 |
| 15��-75�� |
| 2 |
| ||
| 2 |
��2����Ϊcos����+�£�=cos��cos��-sin��sin�£�------��
cos����-�£�=cos��cos��+sin��sin��------�ڡ�5
��+�ڵ�cos����+�£�+cos����-�£�=2cos��cos�£���
���+��=A����-��=B ��=
| A+B |
| 2 |
| A-B |
| 2 |
����۵ã�cosA+cosB=2cos
| A+B |
| 2 |
| A-B |
| 2 |
��3���ɣ�2��֪��y=cos2xcos(2x+
| �� |
| 6 |
| 1 |
| 2 |
| �� |
| 6 |
| �� |
| 6 |
| 1 |
| 2 |
| �� |
| 6 |
| ||
| 4 |
��x��[0��
| �� |
| 4 |
��4x+
| �� |
| 6 |
| �� |
| 6 |
| 7�� |
| 6 |
�ʺ��������ֵΪf(0)=
| ||
| 2 |
��������С����Ҫ�������Ǻ�������Ǻ�����ʽ�������ǹ�ʽ�����Ǻ����ĺ�ȱ任�Ȼ���֪ʶ������������֤����������������������黯����ת��˼��ȣ�

��ϰ��ϵ�д�
�����Ŀ
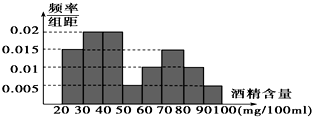 �ݡ�����������������2013��8��1����8��28�գ�ij�н��ܲ��Ź������1000����������ƺ�ݳ������Ƽݳ��ļ�ʻԱ80�ˣ�ͼʾ�Ƕ���80��ѪҺ�оƾ��������м�����ý����Ƶ�ʷֲ�ֱ��ͼ��
�ݡ�����������������2013��8��1����8��28�գ�ij�н��ܲ��Ź������1000����������ƺ�ݳ������Ƽݳ��ļ�ʻԱ80�ˣ�ͼʾ�Ƕ���80��ѪҺ�оƾ��������м�����ý����Ƶ�ʷֲ�ֱ��ͼ�� ����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ���ABEΪ����ֱ�������Σ���BAE=90�㣬��AD��AE��
����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ���ABEΪ����ֱ�������Σ���BAE=90�㣬��AD��AE��