题目内容
已知f(x)=ax2+bx+c的图象过点(-1,0)是否存在常数a,b,c,使得不等式x≤f(x)≤
对一切实数x都成立,若存在,求出a,b,c;若不存在,说明理由.
| 1+x2 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:通过图象过一点得到a、b、c一关系式,观察发现1≤f(1)≤1,又可的一关系式,再将b、c都有a表示.不等式x≤f(x)≤
对一切实数x都成立可转化成两个一元二次不等式恒成立,即可解得.
| 1+x2 |
| 2 |
解答:
解:∵f(x)的图象过点(-1,0),∴a-b+c=0①
∵x≤f(x)≤
对一切x∈R均成立,
∴当x=1时也成立,即1≤a+b+c≤1.
故有a+b+c=1.②
由①②得b=
,c=
-a.
∴f(x)=ax2+
x+
-a.
故x≤ax2+
x+
-a≤
对一切x∈R成立,
也即
恒成立,
即
,
解得a=
.
∴c=
-a=
.
∴常数a,b,c的值为:a=
,b=
,c=
.
∵x≤f(x)≤
| 1+x2 |
| 2 |
∴当x=1时也成立,即1≤a+b+c≤1.
故有a+b+c=1.②
由①②得b=
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=ax2+
| 1 |
| 2 |
| 1 |
| 2 |
故x≤ax2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1+x2 |
| 2 |
也即
|
即
|
解得a=
| 1 |
| 4 |
∴c=
| 1 |
| 2 |
| 1 |
| 4 |
∴常数a,b,c的值为:a=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查了函数恒成立问题,以及二次函数的性质,赋值法(特殊值法)可以使问题变得比较明朗,它是解决这类问题比较常用的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
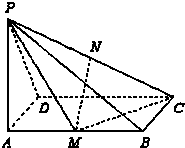 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1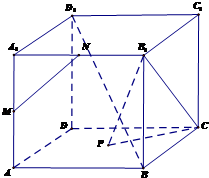 如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,
如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心, 在如图所示的几何体中,四边形ABCD为正方形,△ABE为等腰直角三角形,∠BAE=90°,且AD⊥AE.
在如图所示的几何体中,四边形ABCD为正方形,△ABE为等腰直角三角形,∠BAE=90°,且AD⊥AE.