题目内容
已知函数f(x)=2x2-4x+a,g(x)=logax(a>0且a≠1).
(Ⅰ)若函数f(x)在[-1,2m]上不具有单调性,求实数m的取值范围;
(Ⅱ)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设t1=
f(x),t2=g(x),t3=2x,当x∈(0,1)时,试比较t1,t2,t3的大小.
(Ⅰ)若函数f(x)在[-1,2m]上不具有单调性,求实数m的取值范围;
(Ⅱ)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设t1=
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:综合题,函数的性质及应用
分析:(Ⅰ)可得抛物线的对称轴为x=1,由题意可得-1<1<2m;
(Ⅱ)(i)由题意可得f(1)=0,即-2+a=0;(ii)当x∈(0,1)时,易求t1,t2,t3的取值范围,由范围可得大小关系;
(Ⅱ)(i)由题意可得f(1)=0,即-2+a=0;(ii)当x∈(0,1)时,易求t1,t2,t3的取值范围,由范围可得大小关系;
解答:
解:(Ⅰ)∵抛物线y=2x2-4x+a开口向上,对称轴为x=1,
∴函数f(x)在(-∞,1]单调递减,在[1,+∞)单调递增,
∵函数f(x)在[-1,2m]上不单调,
∴2m>1,得m>
,
∴实数m的取值范围为(
,+∞);
(Ⅱ)(ⅰ)∵f(1)=g(1),
∴-2+a=0,
∴实数a的值为2.
(ⅱ)∵t1=
f(x)=x2-2x+1=(x-1)2,t2=g(x)=log2x,t3=2x,
∴当x∈(0,1)时,t1∈(0,1),t2∈(-∞,0),t3∈(1,2),
∴t2<t1<t3.
∴函数f(x)在(-∞,1]单调递减,在[1,+∞)单调递增,
∵函数f(x)在[-1,2m]上不单调,
∴2m>1,得m>
| 1 |
| 2 |
∴实数m的取值范围为(
| 1 |
| 2 |
(Ⅱ)(ⅰ)∵f(1)=g(1),
∴-2+a=0,
∴实数a的值为2.
(ⅱ)∵t1=
| 1 |
| 2 |
∴当x∈(0,1)时,t1∈(0,1),t2∈(-∞,0),t3∈(1,2),
∴t2<t1<t3.
点评:本题考查二次函数、对数函数、指数函数的性质图象,考查学生灵活运用知识解决问题的能力,属中档题.熟练掌握常见基本函数的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
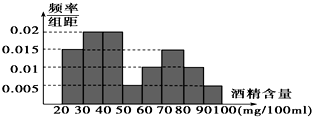 据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.
据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.