题目内容
已知函数f（x）=2sin2（x-
）+
cos2x-3
（1）求函数f（x）的最小正周期；
（2）当x∈[
，
]时，求f（x）的最大值和最小值．
| π |
| 4 |
| 3 |
（1）求函数f（x）的最小正周期；
（2）当x∈[
| π |
| 4 |
| π |
| 2 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法,三角函数的最值
专题：三角函数的求值
分析：（1）由三角函数公式化简可得f（x）=2cos（2x+
）-2，可得周期；
（2）由x的范围结合余弦函数的单调性可得．
| π |
| 6 |
（2）由x的范围结合余弦函数的单调性可得．
解答：
解：（1）化简可得f（x）=2sin2（x-
）+
cos2x-3
=1-cos（2x-
）+
cos2x-3
=-sin2x+
cos2x-2
=2cos（2x+
）-2，
∴函数f（x）的最小正周期T=
=π；
（2）∵x∈[
，
]，∴2x+
∈[
，
]，
∴当2x+
=
，即x=
时，f（x）取最大值-3，
当2x+
=π，即x=
时，f（x）取最小值-4
| π |
| 4 |
| 3 |
=1-cos（2x-
| π |
| 2 |
| 3 |
=-sin2x+
| 3 |
=2cos（2x+
| π |
| 6 |
∴函数f（x）的最小正周期T=
| 2π |
| 2 |
（2）∵x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
∴当2x+
| π |
| 6 |
| 2π |
| 3 |
| π |
| 4 |
当2x+
| π |
| 6 |
| 5π |
| 12 |
点评：本题考查三角函数的化简，涉及三角函数的周期性和最值，属基础题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
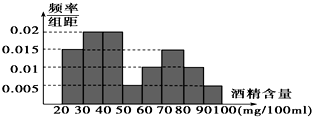据《扬子晚报》报道，2013年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．
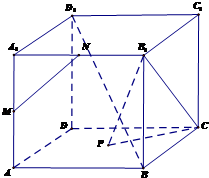如图，已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，
在如图所示的几何体中，四边形ABCD为正方形，△ABE为等腰直角三角形，∠BAE=90°，且AD⊥AE．