题目内容
在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求cosB+cosC的范围.
(1)求A的大小;
(2)求cosB+cosC的范围.
考点:正弦定理
专题:计算题,解三角形
分析:(1)由正弦定理得2a2=(2b+c)b+(2c+b)c,即a2=b2+c2+bc,由余弦定理得a2=b2+c2-2bccosA求出A=120°
(2)根据三角形的内角和为180°,将C用B表示得到cosB+cosC=cosB+cos(60°-B)=cosB+cos60°cosB+sin60°sinB=
sin(60°+B),结合三角函数的图象求出范围.
(2)根据三角形的内角和为180°,将C用B表示得到cosB+cosC=cosB+cos(60°-B)=cosB+cos60°cosB+sin60°sinB=
| 3 |
解答:
解:(1)∵2asinA=(2b+c)sinB+(2c+b)sinC.
由正弦定理得2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc,
由余弦定理得a2=b2+c2-2bccosA
∴cosA=-
,
∴A=120°
(2)cosB+cosC
=cosB+cos(60°-B)
=cosB+cos60°cosB+sin60°sinB
=
cosB+
sinB=
sin(60°+B)
∵0°<B<60°
∴60°<60°+B<120°
∴
<cosB+cosC<
cosB+cosC的范围(
,
)
由正弦定理得2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc,
由余弦定理得a2=b2+c2-2bccosA
∴cosA=-
| 1 |
| 2 |
∴A=120°
(2)cosB+cosC
=cosB+cos(60°-B)
=cosB+cos60°cosB+sin60°sinB
=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
∵0°<B<60°
∴60°<60°+B<120°
∴
| 3 |
| 2 |
| 3 |
cosB+cosC的范围(
| 3 |
| 2 |
| 3 |
点评:本题考查三角形中的正弦定理、余弦定理及它们的应用;考查求三角函数的取值范围,属于一道中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A、B两点.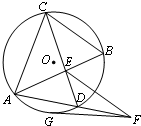 如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证: