题目内容
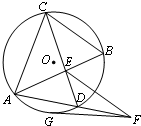如图，E是圆O内两弦AB和CD的交点，过AD延长线上一点F作圆O的切线FG，G为切点，已知EF=FG．求证：（Ⅰ）△DEF∽△EAF；
（Ⅱ）EF∥CB．
考点：与圆有关的比例线段
专题：综合题,立体几何
分析：（Ⅰ）利用切割线定理，EF=FG可得
=
，利用∠EFA=∠DFE，可得△DEF∽△EAF；
（Ⅱ）证明∠FED=∠BCD，即可证明EF∥CB．
| EF |
| FA |
| FD |
| EF |
（Ⅱ）证明∠FED=∠BCD，即可证明EF∥CB．
解答：
证明：（Ⅰ）由切割线定理得FG2=FA•FD．
又EF=FG，所以EF2=FA•FD，即
=
．
因为∠EFA=∠DFE，所以△FED∽△EAF．…（6分）
（Ⅱ）由（Ⅰ）得∠FED=∠FAE．
因为∠FAE=∠DAB=∠DCB，
所以∠FED=∠BCD，所以EF∥CB．…（10分）
证明：（Ⅰ）由切割线定理得FG2=FA•FD．又EF=FG，所以EF2=FA•FD，即
| EF |
| FA |
| FD |
| EF |
因为∠EFA=∠DFE，所以△FED∽△EAF．…（6分）
（Ⅱ）由（Ⅰ）得∠FED=∠FAE．
因为∠FAE=∠DAB=∠DCB，
所以∠FED=∠BCD，所以EF∥CB．…（10分）
点评：本题考查切割线定理，考查三角形相似的判断，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
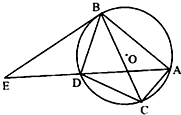（A）如图，△ABC内接圆O，AD平分∠BAC交圆于点D，过点B作圆O的切线交直线AD于点E．