Question

已知二次函数y=-x²+（2m+2）x-（m²+4m-3），m为不小于0的整数，其图象交x轴负半轴于点A，交x轴正半轴于点B
（1）求此二次函数的解析式；
（2）设一次函数y=kx+b的图象过点A并与二次函数的图象交于点C，且△ABC的面积为10，求一次函数的解析式．

Answer 1

考点：二次函数的性质

专题：函数的性质及应用

分析：（1）中由图象交x轴负半轴于点A，交x轴正半轴于点B且m为不小于0的整数，确定m的值，从而求出二次函数的解析式；
（2）由△ABC的面积为10，|AB|=4，求出C点的纵坐标，再代入二次函数的解析式，求出C点坐标，问题宜得．

解答： 解：（1）∵图象交x轴负半轴于点A，交x轴正半轴于点B
∴△=（2m+2）²-4（m²+4m-3）＞0，
解得：m＜2，
又∵m为不小于0的整数，
∴0≤m＜2，m=0或1，
当m=0时，y=-x²+2x+3，其中A（-1，0），B（3，0），
当m=1时，y=-x²+4x-2，不合题意；
∴y=-x²+2x+3．
（2）如图示：

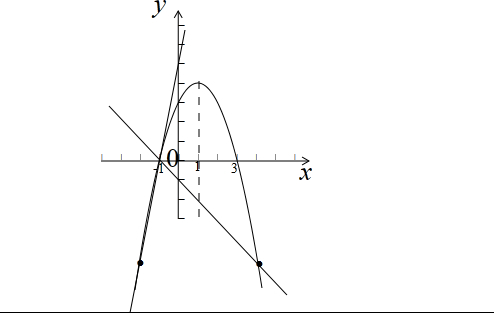
∵△ABC的面积为10，
∴

1

2

|AB|•h=10，
解得：h=5，
∴c点的纵坐标为5（舍）或-5，
把y=-5代入y=-x²+2x+3，
解得：x=4或x=-2，
∴c（4，-5）或（-2，-5），
当A（-1，0），C（4，-5）时，
得：

-k+b=0 4k+b=-5

，∴y=-x-1，
当A（-1，0），C（-2，-5）时，
得：

-k+b=0 -2k+b=-5

∴y=5x+5．
∴所求一次函数的解析式为：y=-x-1，或y=5x+5．

点评：本题考察了二次函数的性质，解方程组，一次函数和二次函数的综合应用，是中档题．