题目内容
△ABC中,三个内角A、B、C所对的边分别为a、b、c,若B=60°,a=(
-1)c.
(Ⅰ)求角A的大小;
(Ⅱ)已知△ABC的面积为12+4
,求函数f(x)=cos2x+asinx的最大值.
| 3 |
(Ⅰ)求角A的大小;
(Ⅱ)已知△ABC的面积为12+4
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(Ⅰ)由B的度数表示出A+C的度数,用A表示出C,已知等式利用正弦定理化简,将表示出的C代入利用两角和与差的正弦函数公式化简,整理后得到tanA=1,即可确定出角A的大小;
(Ⅱ)利用三角形面积公式列出关系式,将表示出的c,sinB以及已知面积代入求出a的值,代入f(x)解析式中化简,利用二次函数的性质及正弦函数的值域即可确定出最大值.
(Ⅱ)利用三角形面积公式列出关系式,将表示出的c,sinB以及已知面积代入求出a的值,代入f(x)解析式中化简,利用二次函数的性质及正弦函数的值域即可确定出最大值.
解答:
解:(Ⅰ)∵B=60°,∴A+C=120°,即C=120°-A,
∵a=(
-1)c,由正弦定理可得:sinA=(
-1)sinC,
sinA=(
-1)sin(120°-A)=(
-1)(
cosA+
sinA),
整理得:
cosA+
sinA-
cosA-
sinA=sinA,
即
cosA=
sinA,
即sinA=cosA,
∴tanA=1,
则A=45°;
(Ⅱ)∵S△ABC=
acsinB=12+4
,c=
,sinB=
,
∴
•
•
=12+4
,
解得:a=4
,
∴f(x)=1-2sin2x+4
sinx=-2(sinx-
)2+5,
则当sinx=1时,函数f(x)取得最大值4
-1.
∵a=(
| 3 |
| 3 |
sinA=(
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
整理得:
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
即
3-
| ||
| 2 |
3-
| ||
| 2 |
即sinA=cosA,
∴tanA=1,
则A=45°;
(Ⅱ)∵S△ABC=
| 1 |
| 2 |
| 3 |
| a | ||
|
| ||
| 2 |
∴
| 1 |
| 2 |
| a2 | ||
|
| ||
| 2 |
| 3 |
解得:a=4
| 2 |
∴f(x)=1-2sin2x+4
| 2 |
| 2 |
则当sinx=1时,函数f(x)取得最大值4
| 2 |
点评:此题考查正弦定理,三角形面积公式,两角和与差的正弦函数公式,二次函数的性质,以及正弦函数的值域,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
已知sin(π+α)=
sin(
-α),且α∈(-π,0),则α=( )
| 3 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知(1+
)2=a+bi(a,b∈R,i为虚数单位),则a+b=
| 2 |
| i |
| A、-4 | B、4 | C、-7 | D、7 |
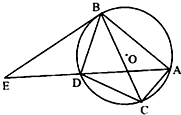 (A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E.
(A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E. 2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表:
2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表: