题目内容
在△ABC中,a,b,c分别是角A,B,C的对边.已知a=2
,A=
.
(Ⅰ)若b=2
,求角C的大小;
(Ⅱ)若c=2,求边b的长.
| 3 |
| π |
| 3 |
(Ⅰ)若b=2
| 2 |
(Ⅱ)若c=2,求边b的长.
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)根据正弦定理和已知条件求得sinB的值,进而求得B,最后利用三角形内角和求得C.
(Ⅱ)用余弦定理列出关于b的表达式,整理求得b.
(Ⅱ)用余弦定理列出关于b的表达式,整理求得b.
解答:
解:(Ⅰ)由正弦定理
=
,
∴sinB=
•sinA=
×
=
,
∴B=
或
,
∵b<a,
∴B=
,
∴C=π-
-
=
.
(Ⅱ)依题意,cosA=
,即
=
.
∴b2-2b-8=0,
又b>0,
∴b=4.
| a |
| sinA |
| b |
| sinB |
∴sinB=
| b |
| a |
2
| ||
2
|
| ||
| 2 |
| ||
| 2 |
∴B=
| π |
| 4 |
| 3π |
| 4 |
∵b<a,
∴B=
| π |
| 4 |
∴C=π-
| π |
| 3 |
| π |
| 4 |
| 5π |
| 12 |
(Ⅱ)依题意,cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| b2+4-12 |
| 4b |
∴b2-2b-8=0,
又b>0,
∴b=4.
点评:本题主要考查了正弦定理和余弦定理的综合运用.灵活运用正弦和余弦定理解三角形问题.

练习册系列答案
相关题目
已知i为虚数单位,若(1+i)(2-i)=a+i,则实数a的值为( )
| A、-1 | B、1 | C、-3 | D、3 |
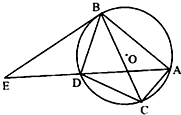 (A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E.
(A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E.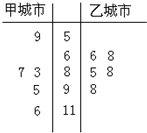 2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表:
2014年“雾霾”成为年度关键词.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”. PM2.5日均值越小,空气质量越好.下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表: