题目内容
设
，
是平面内两个不共线的向量，
=（a-1）
+
，
=b
-2
（a＞0，b＞0），若A，B，C三点共线，则ab的最大值是（ ）
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| AC |
| e1 |
| e2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平行向量与共线向量,基本不等式
专题：平面向量及应用
分析：根据向量的共线的性质得到b=2-2a，再利用二次函数求最大值．
解答：
解：若A，B，C三点共线，则
=λ
，
∴（a-1）
+
=λ（b
-2
），
即：
，
∴b=2-2a
∴ab=a（2-2a）=2a-2a2═-2(a-
)2+
当a=
，b=1，ab有最大值，最大值为
．
故选B
| AB |
| AC |
∴（a-1）
| e1 |
| e2 |
| e1 |
| e2 |
即：
|
∴b=2-2a
∴ab=a（2-2a）=2a-2a2═-2(a-
| 1 |
| 2 |
| 1 |
| 2 |
当a=
| 1 |
| 2 |
| 1 |
| 2 |
故选B
点评：本题主要考查了向量的三点共线问题，以及利用配方法求最值的问题，属于基础题．
练习册系列答案
相关题目
已知sin（π+α）=
sin（
-α），且α∈（-π，0），则α=（ ）
| 3 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知i为虚数单位，若（1+i）（2-i）=a+i，则实数a的值为（ ）
| A、-1 | B、1 | C、-3 | D、3 |
若
=1-bi，（其中a，b都是实数，i是虚数单位），则|a+bi|=（ ）
| a |
| 1-i |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知（1+
）2=a+bi（a，b∈R，i为虚数单位），则a+b=
| 2 |
| i |
| A、-4 | B、4 | C、-7 | D、7 |
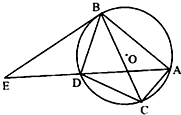（A）如图，△ABC内接圆O，AD平分∠BAC交圆于点D，过点B作圆O的切线交直线AD于点E．