题目内容
函数y=
的值域为( )
x-
| ||
| x+|1-x| |
| A、(-∞,1) |
| B、(-∞,1] |
| C、(0,1] |
| D、[0,1] |
考点:函数的值域
专题:函数的性质及应用
分析:通过换元t=
,则x=1-t2,
y=-t2-t+1,t∈[0,+∞),转化为二次函数求解即可.
| 1-x |
y=-t2-t+1,t∈[0,+∞),转化为二次函数求解即可.
解答:
解;设t=
,则x=1-t2,
y=-t2-t+1,t∈[0,+∞),
∵轴t=-
,可判断在t∈[0,+∞)上单调递减,
∴当t=0时,y=1,
故选:B
| 1-x |
y=-t2-t+1,t∈[0,+∞),
∵轴t=-
| 1 |
| 2 |
∴当t=0时,y=1,
故选:B
点评:本题考查了二次函数的性质,注意变量的范围.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
若复数z=(
)2014,则ln|z|=( )
| 1+i |
| 1-i |
| A、-2 | B、0 | C、1 | D、不存在 |
已知偶函数f(x)满足f(-1)=0,且在区间[0,+∞)上为减函数,不等式f(log2x)>0的解集为( )
| A、(-1,1) | ||
| B、(-∞,-1)∪(1,+∞) | ||
C、(
| ||
D、(0,
|
设y1=40.9,y2=80.5,y3=(
)-1.6,则( )
| 1 |
| 2 |
| A、y3>y1>y2 |
| B、y2>y1>y3 |
| C、y1>y2>y3 |
| D、y1>y3>y2 |
过点A(1,2)且与原点距离最大的直线方程为( )
| A、2x+y-4=0 |
| B、x+2y-5=0 |
| C、x+3y-7=0 |
| D、3x+y-5=0 |
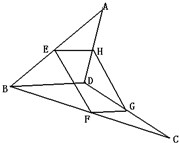 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.