题目内容
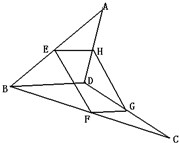如图，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形，求证：BD∥面EFGH．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：利用线面平行的判定和性质定理即可证明．
解答：
解：∵截面EFGH是平行四边形，∴EH∥GF，
∵EH?平面BCD，FG?平面BCD，
∴EH∥平面BCD．
∵平面ABD∩平面BCD=BD．
∴EH∥BD．
∵EH?平面EFGH，BD?平面EFGH，
∴BD∥平面EFGH．
∵EH?平面BCD，FG?平面BCD，
∴EH∥平面BCD．
∵平面ABD∩平面BCD=BD．
∴EH∥BD．
∵EH?平面EFGH，BD?平面EFGH，
∴BD∥平面EFGH．
点评：熟练掌握线面平行的判定和性质定理是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的值域为（ ）
x-
| ||
| x+|1-x| |
| A、（-∞，1） |
| B、（-∞，1] |
| C、（0，1] |
| D、[0，1] |
函数f（x）=x2-2mx与g（x）=
在区间[1，2]上都是减函数，则m的取值范围是（ ）
| mx+3 |
| x+1 |
| A、[2，3） |
| B、[2，3] |
| C、[2，+∞） |
| D、（-∞，3） |
函数y=
在区间（0，+∞）上是增函数，则实数m的取值范围是（ ）
| 1-3m |
| x |
A、m＞
| ||
B、m≥
| ||
C、m＜
| ||
D、m≤
|