题目内容
已知过点A(0,b),且斜率为1的直线l与圆O:x2+y2=16交于不同的两点M、N.
(Ⅰ)求实数b的取值范围;
(Ⅱ)当△MON的面积最大时,求实数b的值;
(Ⅲ)设关于x的一元二次方程x2+2ax-b2+16=0,若a、b是从区间[-4,4]上任取的两 个数,求上述方程有实根的概率.
(Ⅰ)求实数b的取值范围;
(Ⅱ)当△MON的面积最大时,求实数b的值;
(Ⅲ)设关于x的一元二次方程x2+2ax-b2+16=0,若a、b是从区间[-4,4]上任取的两 个数,求上述方程有实根的概率.
考点:直线与圆的位置关系
专题:综合题,直线与圆
分析:(Ⅰ)直线l与圆O:x2+y2=16交于不同的两点M、N,圆心到直线l的距离d=
<4,可得实数b的取值范围;
(Ⅱ)S△MON=
×2
×d,利用基本不等式,确定△MON的面积最大,即可求实数b的值;
(Ⅲ)试验的全部结果构成的区域为:{(a,b)|-4≤a≤4,-4≤b≤4},是边长为8的正方形满足题意的区域为:{(a,b)|a2+b2≥16,-4≤a≤4,-4≤b≤4},分别求解区域的面积,可求方程有实根的概率.
| |b| | ||
|
(Ⅱ)S△MON=
| 1 |
| 2 |
| 16-d2 |
(Ⅲ)试验的全部结果构成的区域为:{(a,b)|-4≤a≤4,-4≤b≤4},是边长为8的正方形满足题意的区域为:{(a,b)|a2+b2≥16,-4≤a≤4,-4≤b≤4},分别求解区域的面积,可求方程有实根的概率.
解答:
解:(Ⅰ)设直线l:x-y+b=0,
∵直线l与圆O:x2+y2=16交于不同的两点M、N,
∴圆心到直线l的距离d=
<4,
∴-4
<b<4
;
(Ⅱ)∵|MN|=2
,
∴S△MON=
×2
×d≤
=8,
当且仅当16-d2=d2,即d=2
时,△MON的面积最大,此时b=±4;
( III)试验的全部结果所构成的区域为:{(a,b)|-4≤a≤4,-4≤b≤4},是边长为8的正方形;
记事件C为“一元二次方程x2+2ax-b2+16=0有实根”,
因为方程x2+2ax-b2+16=0有实根,
即△=(2a)2-4(-b2+16)=4a2+4b2-64≥0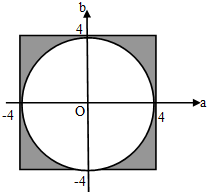
即a2+b2≥16,
故构成事件A的区域为:{(a,b)|a2+b2≥16,-4≤a≤4,-4≤b≤4},
即图中的阴影部分
这是一个几何概型,所以
P(C)=
=
=1-
;
即一元二次方程x2+2ax-b2+16=0有实根的概率为1-
.
∵直线l与圆O:x2+y2=16交于不同的两点M、N,
∴圆心到直线l的距离d=
| |b| | ||
|
∴-4
| 2 |
| 2 |
(Ⅱ)∵|MN|=2
| 16-d2 |
∴S△MON=
| 1 |
| 2 |
| 16-d2 |
| 16-d2+d2 |
| 2 |
当且仅当16-d2=d2,即d=2
| 2 |
( III)试验的全部结果所构成的区域为:{(a,b)|-4≤a≤4,-4≤b≤4},是边长为8的正方形;
记事件C为“一元二次方程x2+2ax-b2+16=0有实根”,
因为方程x2+2ax-b2+16=0有实根,
即△=(2a)2-4(-b2+16)=4a2+4b2-64≥0

即a2+b2≥16,
故构成事件A的区域为:{(a,b)|a2+b2≥16,-4≤a≤4,-4≤b≤4},
即图中的阴影部分
这是一个几何概型,所以
P(C)=
| S阴影 |
| S正方形 |
| 82-π•42 |
| 82 |
| π |
| 4 |
即一元二次方程x2+2ax-b2+16=0有实根的概率为1-
| π |
| 4 |
点评:本题考查直线与圆的位置关系,考查基本不等式的运用,考查概率知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C关于y轴对称,经过点(1,0)且被x轴分成两段弧长比为1:2,则圆C的方程为( )
A、(x±
| ||||||
B、(x±
| ||||||
C、x2+(y±
| ||||||
D、x2+(y±
|
函数y=
的值域为( )
x-
| ||
| x+|1-x| |
| A、(-∞,1) |
| B、(-∞,1] |
| C、(0,1] |
| D、[0,1] |
函数f(x)=x2-2mx与g(x)=
在区间[1,2]上都是减函数,则m的取值范围是( )
| mx+3 |
| x+1 |
| A、[2,3) |
| B、[2,3] |
| C、[2,+∞) |
| D、(-∞,3) |
函数y=
在区间(0,+∞)上是增函数,则实数m的取值范围是( )
| 1-3m |
| x |
A、m>
| ||
B、m≥
| ||
C、m<
| ||
D、m≤
|